《2019-2020學(xué)年新教材高中數(shù)學(xué) 第3章 函數(shù)的概念與性質(zhì) 章末復(fù)習(xí)教學(xué)案 新人教A版必修第一冊》由會員分享,可在線閱讀����,更多相關(guān)《2019-2020學(xué)年新教材高中數(shù)學(xué) 第3章 函數(shù)的概念與性質(zhì) 章末復(fù)習(xí)教學(xué)案 新人教A版必修第一冊(7頁珍藏版)》請在裝配圖網(wǎng)上搜索����。
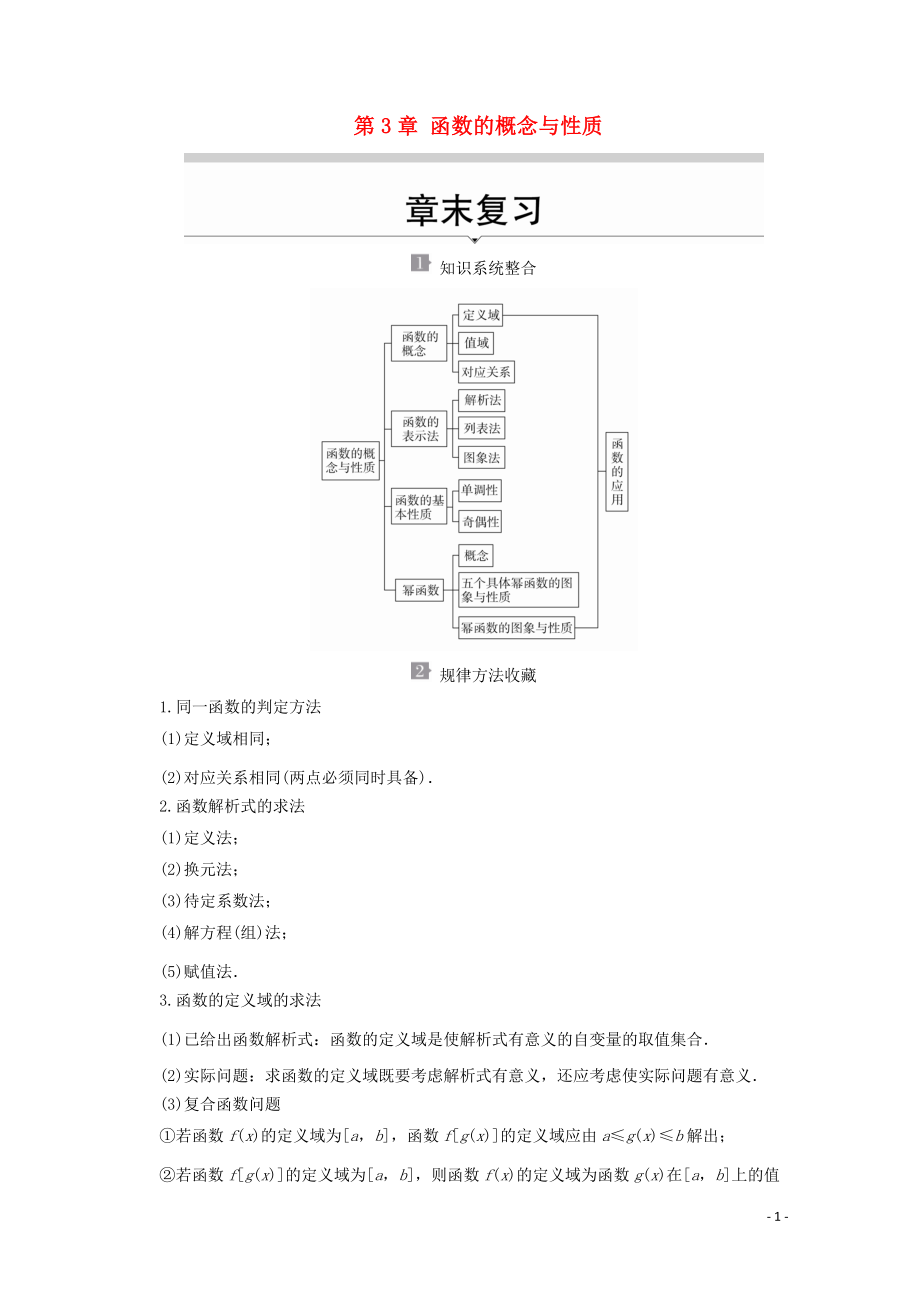
1、第3章 函數(shù)的概念與性質(zhì) 知識系統(tǒng)整合 規(guī)律方法收藏1.同一函數(shù)的判定方法(1)定義域相同;(2)對應(yīng)關(guān)系相同(兩點必須同時具備)2.函數(shù)解析式的求法(1)定義法����;(2)換元法���;(3)待定系數(shù)法���;(4)解方程(組)法��;(5)賦值法3.函數(shù)的定義域的求法(1)已給出函數(shù)解析式:函數(shù)的定義域是使解析式有意義的自變量的取值集合(2)實際問題:求函數(shù)的定義域既要考慮解析式有意義���,還應(yīng)考慮使實際問題有意義(3)復(fù)合函數(shù)問題若函數(shù)f(x)的定義域為a,b�,函數(shù)fg(x)的定義域應(yīng)由ag(x)b解出����;若函數(shù)fg(x)的定義域為a�����,b���,則函數(shù)f(x)的定義域為函數(shù)g(x)在a,b上的值域注意:函數(shù)f(x)中的
2�����、x與函數(shù)fg(x)中的g(x)地位相同定義域所指永遠(yuǎn)是x的范圍4.函數(shù)值域的求法(1)配方法(二次或四次)���;(2)判別式法�����;(3)換元法��;(4)函數(shù)的單調(diào)性法5.判斷函數(shù)單調(diào)性的步驟(1)設(shè)x1�,x2是所研究區(qū)間內(nèi)任意兩個自變量的值,且x1x2;(2)判定f(x1)與f(x2)的大?�。鹤鞑畋容^或作商比較����;(3)根據(jù)單調(diào)性定義下結(jié)論6.函數(shù)奇偶性的判定方法首先考查函數(shù)的定義域是否關(guān)于原點對稱�,再看函數(shù)f(x)與f(x)之間的關(guān)系:若函數(shù)f(x)f(x)�����,則f(x)為偶函數(shù)����;若函數(shù)f(x)f(x)���,則f(x)為奇函數(shù)�;若f(x)f(x)0����,則f(x)為偶函數(shù);若f(x)f(x)0,則f(x)為奇函
3�����、數(shù)��;若1(f(x)0)�����,則f(x)為偶函數(shù)��;若1(f(x)0)��,則f(x)為奇函數(shù)7.冪函數(shù)的圖象特征(1)冪函數(shù)的圖象一定會出現(xiàn)在第一象限內(nèi),一定不會出現(xiàn)在第四象限內(nèi)��,圖象最多只能同時出現(xiàn)在兩個象限內(nèi)��,至于是否在第二、三象限內(nèi)出現(xiàn)�,則要看冪函數(shù)的奇偶性(2)冪函數(shù)的圖象在第一象限內(nèi)的變化規(guī)律為:在第一象限內(nèi)直線x1的右側(cè),圖象從下到上,相應(yīng)的指數(shù)由小到大����,直線x1的左側(cè)����,圖象從下到上,相應(yīng)的指數(shù)由大到小8.函數(shù)的應(yīng)用解決函數(shù)應(yīng)用題關(guān)鍵在于理解題意�����,提高閱讀能力一方面要加強對常見函數(shù)模型的理解���,弄清其產(chǎn)生的實際背景��,把數(shù)學(xué)問題生活化��;另一方面����,要不斷拓寬知識面����,增加間接的生活閱歷����,諸如了解一些
4、物價、行程���、產(chǎn)值���、利潤����、環(huán)保等實際問題,及有關(guān)角度�����、面積�����、體積�����、造價的問題��,培養(yǎng)實際問題數(shù)學(xué)化的意識和能力 學(xué)科思想培優(yōu)一�、函數(shù)的定義域函數(shù)的定義域是指函數(shù)yf(x)中自變量x的取值范圍確定函數(shù)的定義域是進(jìn)一步研究函數(shù)其他性質(zhì)的前提��,而研究函數(shù)的性質(zhì)�����,利用函數(shù)的性質(zhì)解決數(shù)學(xué)問題是中學(xué)數(shù)學(xué)的重要組成部分所以熟悉函數(shù)定義域的求法�,對于函數(shù)綜合問題的解決起著至關(guān)重要的作用典例1(1)函數(shù)f(x)(3x1)0的定義域是()A. B.C. D.(2)已知函數(shù)yf(x1)的定義域是2,3,則yf(2x1)的定義域是()A. B1,4C.5,5 D3,7解析(1)由題意��,得解得x1且x.(2)設(shè)ux1����,由2
5��、x3�,得1x14����,所以yf(u)的定義域為1,4再由12x14�����,解得0x���,即函數(shù)yf(2x1)的定義域是.答案(1)D(2)A二��、分段函數(shù)問題所謂分段函數(shù)是指在定義域的不同子區(qū)間上的對應(yīng)關(guān)系不同的函數(shù)分段函數(shù)是一個函數(shù)而非幾個函數(shù)��,其定義域是各子區(qū)間的并集�,值域是各段上值域的并集分段函數(shù)求值等問題是高考?�?嫉膯栴}典例2已知實數(shù)a0�,函數(shù)f(x)若f(1a)f(1a)�����,則a的值為_解析當(dāng)1a0時,此時a11����,由f(1a)f(1a),得2(1a)a(1a)2a���,解得a(舍去)����;當(dāng)1a1,即a0時���,此時a10.(1)判定函數(shù)f(x)的奇偶性�����;(2)判定函數(shù)f(x)在(1,0)上的單調(diào)性解(1)令xy
6�、0,得2f(0)f(0)��,f(0)0.再令yx��,得f(x)f(x)f(0)0,f(x)f(x)����,f(x)在(1,1)上是奇函數(shù)(2)設(shè)1x1x20.f(x2)f(x1)f(x2)f(x1)f.1x1x20,1x20,且0x1x21���,01x1x20.x2x11x1x2(x21)x1(x21)(1x1)(x21)0��,0x2x11x1x2���,00,且f(x)為奇函數(shù)�����,x(0,1)時���,f(x)0�����,f(x2)f(x1)0�����,即f(x2)f(x1)f(x)在(1,0)上單調(diào)遞減四���、函數(shù)圖象及應(yīng)用函數(shù)的圖象是函數(shù)的重要表示方法�����,它具有明顯的直觀性,通過函數(shù)的圖象能夠掌握函數(shù)重要的性質(zhì)��,如單調(diào)性��、奇偶性等反之���,掌
7、握好函數(shù)的性質(zhì)����,有助于函數(shù)圖象正確地畫出函數(shù)圖象廣泛應(yīng)用于解題過程中�,利用數(shù)形結(jié)合解題具有直觀、明了��、易懂的優(yōu)點典例4設(shè)函數(shù)f(x)x22|x|1(3x3)(1)證明:函數(shù)f(x)是偶函數(shù)�����;(2)畫出這個函數(shù)的圖象�;(3)指出函數(shù)f(x)的單調(diào)區(qū)間�,并說明在各個單調(diào)區(qū)間上f(x)的單調(diào)性;(4)求函數(shù)的值域解(1)證明:函數(shù)f(x)的定義域關(guān)于原點對稱���,且f(x)(x)22|x|1x22|x|1f(x)���,即f(x)f(x),f(x)是偶函數(shù)(2)當(dāng)0x3時���,f(x)x22x1(x1)22.當(dāng)3x0時����,f(x)x22x1(x1)22.即f(x)根據(jù)二次函數(shù)的作圖方法,可得函數(shù)圖象如下圖(3)函數(shù)
8��、f(x)的單調(diào)區(qū)間為3,1)����,1,0),0,1)���,1,3f(x)在區(qū)間3���,1)和0,1)上單調(diào)遞減�����,在1,0)和1,3上單調(diào)遞增(4)當(dāng)0x3時�,函數(shù)f(x)(x1)22的最小值為2,最大值為f(3)2�����;當(dāng)3x0時�����,函數(shù)f(x)(x1)22的最小值為2����,最大值為f(3)2.故函數(shù)f(x)的值域為2,2.五���、冪函數(shù)的圖象問題對于給定的冪函數(shù)圖象����,能從函數(shù)圖象的分布�、變化趨勢、對稱性等方面研究函數(shù)的定義域��、值域����、單調(diào)性、奇偶性等性質(zhì)注意圖象與函數(shù)解析式中指數(shù)的關(guān)系���,能夠根據(jù)圖象比較指數(shù)的大小 典例5如圖是冪函數(shù)yxa���,yxb����,yxc����,yxd在第一象限內(nèi)的圖象,則a����,b���,c��,d的大小關(guān)系為()A.a
9��、bcdB.abdcC.bacdD.badc解析由冪函數(shù)的圖象特征可知�,在第一象限內(nèi)直線x1的右側(cè),圖象從下到上���,相應(yīng)的指數(shù)由小到大故選A.答案A六、函數(shù)模型及其應(yīng)用建立恰當(dāng)?shù)暮瘮?shù)模型解決實際問題的步驟:(1)對實際問題進(jìn)行抽象概括���,確定變量之間的主被動關(guān)系�,并用x,y分別表示�����;(2)建立函數(shù)模型,將變量y表示為x的函數(shù),此時要注意函數(shù)的定義域�����;(3)求解函數(shù)模型�����,并還原為實際問題的解典例6已知A���,B兩城市相距100 km�����,在兩地之間距離A城市x km的D處修建一垃圾處理廠來解決A���,B兩城市的生活垃圾和工業(yè)垃圾為保證不影響兩城市的環(huán)境����,垃圾處理廠與市區(qū)距離不得少于10 km.已知垃圾處理費用和距離的平方與垃圾量之積的和成正比,比例系數(shù)為0.25.若A城市每天產(chǎn)生的垃圾量為20 t���,B城市每天產(chǎn)生的垃圾量為10 t(1)求x的取值范圍����;(2)把每天的垃圾處理費用y表示成x的函數(shù)��;(3)垃圾處理廠建在距離A城市多遠(yuǎn)處���,才能使每天的垃圾處理費用最少�?解(1)由題意可得x10,100x10.所以10x90.所以x的取值范圍為10,90(2)由題意�����,得y0.2520x210(100x)2,即yx2500x25000(10x90)(3)由yx2500x250002(10x90)���,則當(dāng)x時��,y最小即當(dāng)垃圾處理廠建在距離A城市 km時��,才能使每天的垃圾處理費用最少- 7 -
 2019-2020學(xué)年新教材高中數(shù)學(xué) 第3章 函數(shù)的概念與性質(zhì) 章末復(fù)習(xí)教學(xué)案 新人教A版必修第一冊
2019-2020學(xué)年新教材高中數(shù)學(xué) 第3章 函數(shù)的概念與性質(zhì) 章末復(fù)習(xí)教學(xué)案 新人教A版必修第一冊