《2.3《公式法》教案（北師大版九年級上）（7套）-公式法 教案 (1)doc--初中數(shù)學(xué)》由會員分享，可在線閱讀，更多相關(guān)《2.3《公式法》教案（北師大版九年級上）（7套）-公式法 教案 (1)doc--初中數(shù)學(xué)（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。
1、 永久免費在線組卷 課件教案下載 無需注冊和點數(shù)
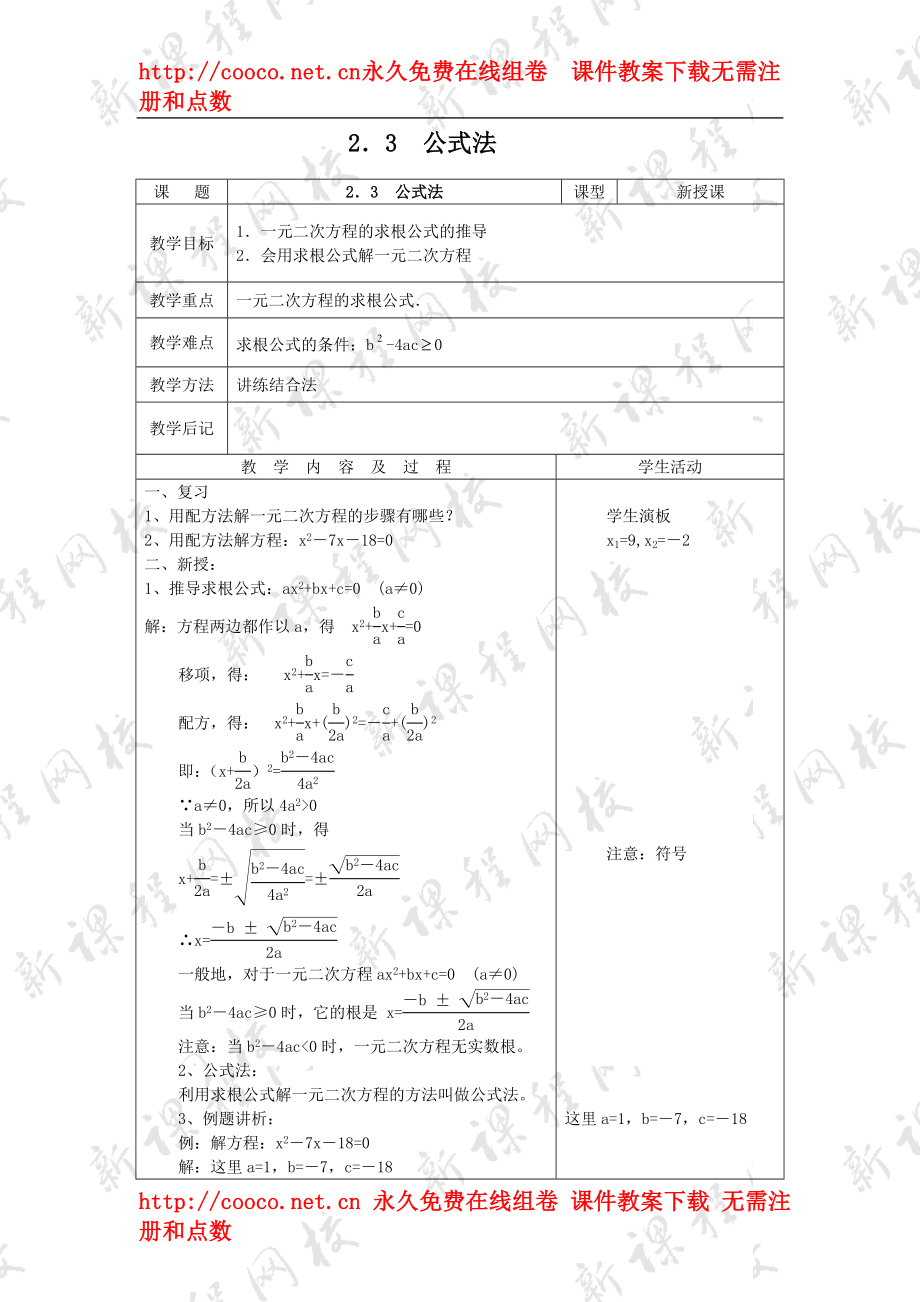
2．3 公式法
課 題
2．3 公式法
課型
新授課
教學(xué)目標(biāo)
1．一元二次方程的求根公式的推導(dǎo)
2．會用求根公式解一元二次方程
教學(xué)重點
一元二次方程的求根公式．
教學(xué)難點
求根公式的條件：b-4ac0
教學(xué)方法
講練結(jié)合法
教學(xué)后記
教 學(xué) 內(nèi) 容 及 過 程
學(xué)生活動
一、復(fù)習(xí)
1、用配方法解一元二次方程的步驟有哪些？
2、用配方法解方程：x2－7x－18=0
二、新授：
1、推導(dǎo)求根公式：ax2+bx+c=0 (a≠0)
解：方程兩邊都作以a，得 x2+x
2、+=0
移項，得： x2+x=－
配方，得： x2+x+()2=－+()2
即：（x+）2=
∵a≠0，所以4a2>0
當(dāng)b2－4ac≥0時，得
x+=±=±
∴x=
一般地，對于一元二次方程ax2+bx+c=0 (a≠0)
當(dāng)b2－4ac≥0時，它的根是 x=
注意：當(dāng)b2－4ac<0時，一元二次方程無實數(shù)根。
2、公式法：
利用求根公式解一元二次方程的方法叫做公式法。
3、例題講析：
例：解方程：x2―7x―18=0
解：這里a=1，b=―7，c=―18
∵b2－4ac=(―7)2―4×1×(―18)=121>0
∴x= 即：x1=9, x2
3、=―2
例：解方程：2x2+7x=4
解：移項，得2x2+7x―4=0
這里，a=1 , b=7 , c=―4
∵b2－4ac=72―4×1×(―4)=81>0
∴x==
即:x1= , x2=―4
三、鞏固練習(xí)：
P58隨堂練習(xí)：1、2
四、小結(jié)：
（1）求根公式：x= （b2－4ac≥0）
（2）利用求根公式解一元二次方程的步驟
五、作業(yè)：
（一）P59 習(xí)題2.6 1、2
（二）預(yù)習(xí)內(nèi)容：P59～P61
板書設(shè)計：
一、 復(fù)習(xí)
二、 求根公式的推導(dǎo)
三、 練習(xí)
四、 小結(jié)
五、
4、 作業(yè)
學(xué)生演板
x1=9,x2=－2
注意：符號
這里a=1，b=―7，c=―18
學(xué)生小結(jié)
步驟: (1)指出a、b、c
（2）求出b2－4ac
(3)求x
（4）求x1, x2
看課本P56～P57，然后小結(jié)
這節(jié)課我們探討了一元二次方程的另一種解法――公式法。
（1）求根公式的推導(dǎo)，實際上是“配方”與“開平方”的綜合應(yīng)用。對于a0，知4a>0等條件在推導(dǎo)過程中的應(yīng)用，也要弄清其中的道理。
（2）應(yīng)用求根公式解一元二次方程，通常應(yīng)把方程寫成一般形式，并寫出a、b、c的數(shù)值以及計算b－4ac的值。當(dāng)熟練掌握求根公式后，可以簡化求解過程
永久免費在線組卷 課件教案下載 無需注冊和點數(shù)
2.3《公式法》教案（北師大版九年級上）（7套）-公式法 教案 (1)doc--初中數(shù)學(xué)
