《浙江省2013年中考數(shù)學一輪復習 考點跟蹤訓練47 方程與函數(shù)相結合型綜合問題(無答案)》由會員分享,可在線閱讀�,更多相關《浙江省2013年中考數(shù)學一輪復習 考點跟蹤訓練47 方程與函數(shù)相結合型綜合問題(無答案)(3頁珍藏版)》請在裝配圖網上搜索。
1、考點跟蹤訓練47 方程與函數(shù)相結合型綜合問題
一���、選擇題(每小題6分���,共30分)
1.在平面直角坐標系中,拋物線y=x2-1與x軸的交點的個數(shù)是( )
A.3 B.2
C.1 D.0
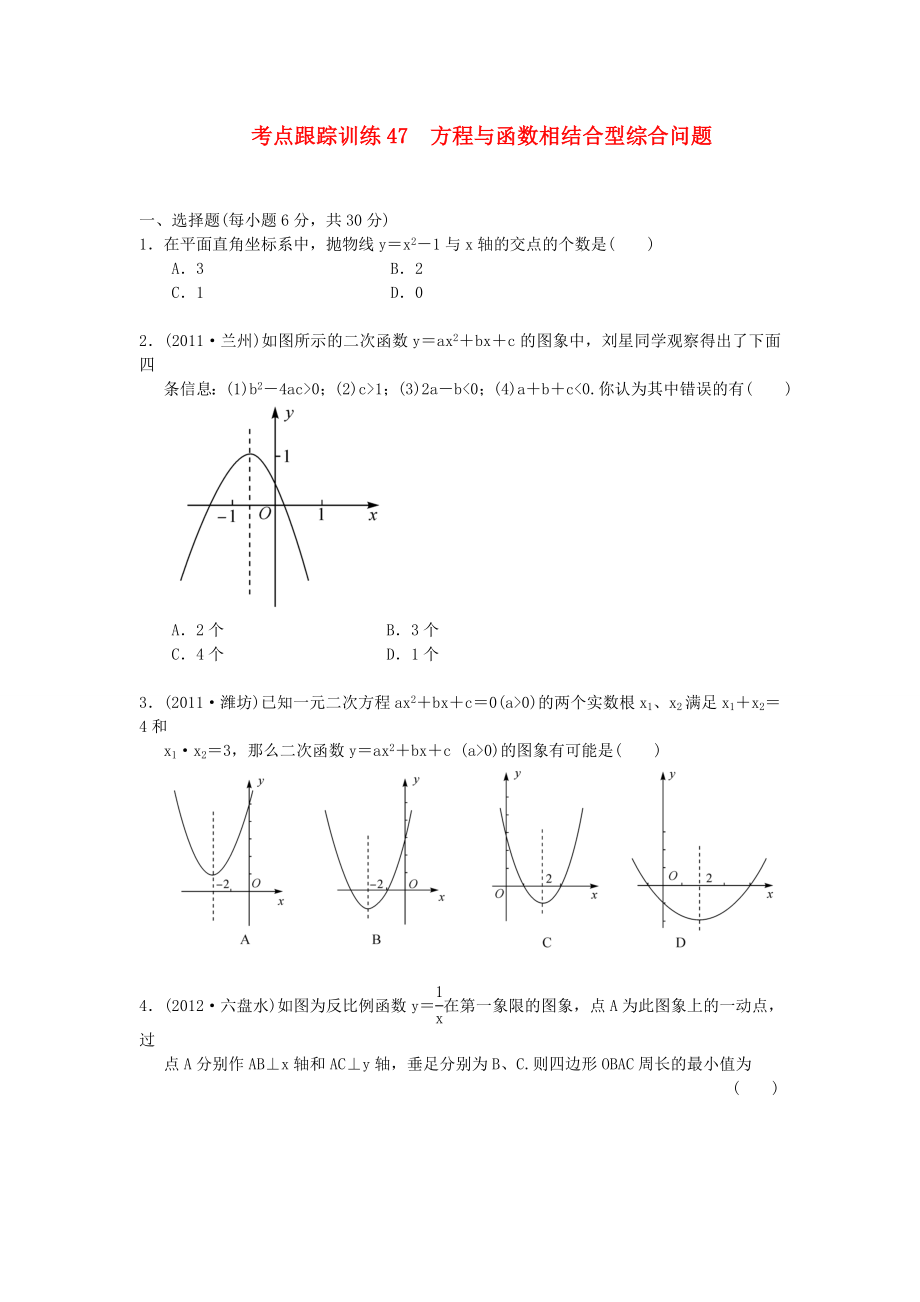
2.(2011·蘭州)如圖所示的二次函數(shù)y=ax2+bx+c的圖象中��,劉星同學觀察得出了下面四
條信息:(1)b2-4ac>0����;(2)c>1;(3)2a-b<0��;(4)a+b+c<0.你認為其中錯誤的有( )
A.2個 B.3個
C.
2���、4個 D.1個
3.(2011·濰坊)已知一元二次方程ax2+bx+c=0(a>0)的兩個實數(shù)根x1��、x2滿足x1+x2=4和
x1·x2=3�,那么二次函數(shù)y=ax2+bx+c (a>0)的圖象有可能是( )
4.(2012·六盤水)如圖為反比例函數(shù)y=在第一象限的圖象��,點A為此圖象上的一動點�,過
點A分別作AB⊥x軸和AC⊥y軸,垂足分別為B����、C.則四邊形OBAC周長的最小值為
3����、 ( )
A.4 B.3
C.2 D.1
5.(2012·樂山)二次函數(shù)y=ax2+bx+1(a≠0)的圖象的頂點在第一象限����,且過點(-1���,0).設
t=a+b+1�,則t值的變化范圍是( )
A.0<t<1 B.0<t<2
C.1<t<2 D.-1<t<1
二��、填空題(每小題6分��,共30分)
6.(2012·恩施)如圖��,直線y=kx+b經過A(3�����,1)和B(6���,0)兩點�����,則不等式組0<kx+b<x
4���、的解集為________.
7.已知關于x的分式方程 =1的解是非正數(shù)�����,則a的取值范圍是________.
8.(2012·荊門)新定義:[a�����,b]為一次函數(shù)y=ax+b(a≠0����,a��、b為實數(shù))的“關聯(lián)數(shù)”.若
“關聯(lián)數(shù)”[1��,m-2]的一次函數(shù)是正比例函數(shù)�����,則關于x的方程+=1的解為
______________.
9.(2012·黔東南)設函數(shù)y=x-3與y=的圖象的兩個交點的橫坐標為a���、b����,則+=
________.
10.(2012·蘇州)如圖,已知第一象限內的圖象是反比例函數(shù)y=圖象的一個分支���,第二象
限內的圖象是反比例函數(shù)y=-
5、圖象的一個分支���,在x軸的上方有一條平行于x軸的
直線l與它們分別交于點A���、B,過點A���、B作x軸的垂線�,垂足分別為C�、D.若四邊
形ABCD的周長為8且AB<AC,則點A的坐標為________.
三����、解答題(每小題20分,共40分)
11.如果一個二次函數(shù)的圖象經過點A(6�,10)����,與x軸交于B��、C兩點���,點B�����、C的橫坐標
為x1��、x2��,且x1+x2=6�����,x1·x2=5.求這個二次函數(shù)的解析式.
12.(2012·樂山)已知關于x的一元二次方程(x-m)2+6x=4m-3有實數(shù)根.
(1)求m的取值范圍���;
(2)設方程的兩實根分別為x1與x2,求代數(shù)式x1·x2-x-x的最大值.
四��、附加題(共20分)
13.(2012·梅州)(1)已知一元二次方程x2+px+q=0(p2-4q≥0)的兩根為x1��、x2.求證:x1+
x2=-p,x1·x2=q�;
(2)已知拋物線y=x2+px+q與x軸交于A、B兩點���,且過點(-1����,-1)�,設線段AB的
長為d,當p為何值時����,d2取得最小值��,并求出最小值.
 浙江省2013年中考數(shù)學一輪復習 考點跟蹤訓練47 方程與函數(shù)相結合型綜合問題(無答案)
浙江省2013年中考數(shù)學一輪復習 考點跟蹤訓練47 方程與函數(shù)相結合型綜合問題(無答案)