《2010高考數(shù)學(xué)導(dǎo)學(xué)練系列 復(fù)數(shù)教案 蘇教版》由會(huì)員分享�,可在線閱讀,更多相關(guān)《2010高考數(shù)學(xué)導(dǎo)學(xué)練系列 復(fù)數(shù)教案 蘇教版(9頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�。
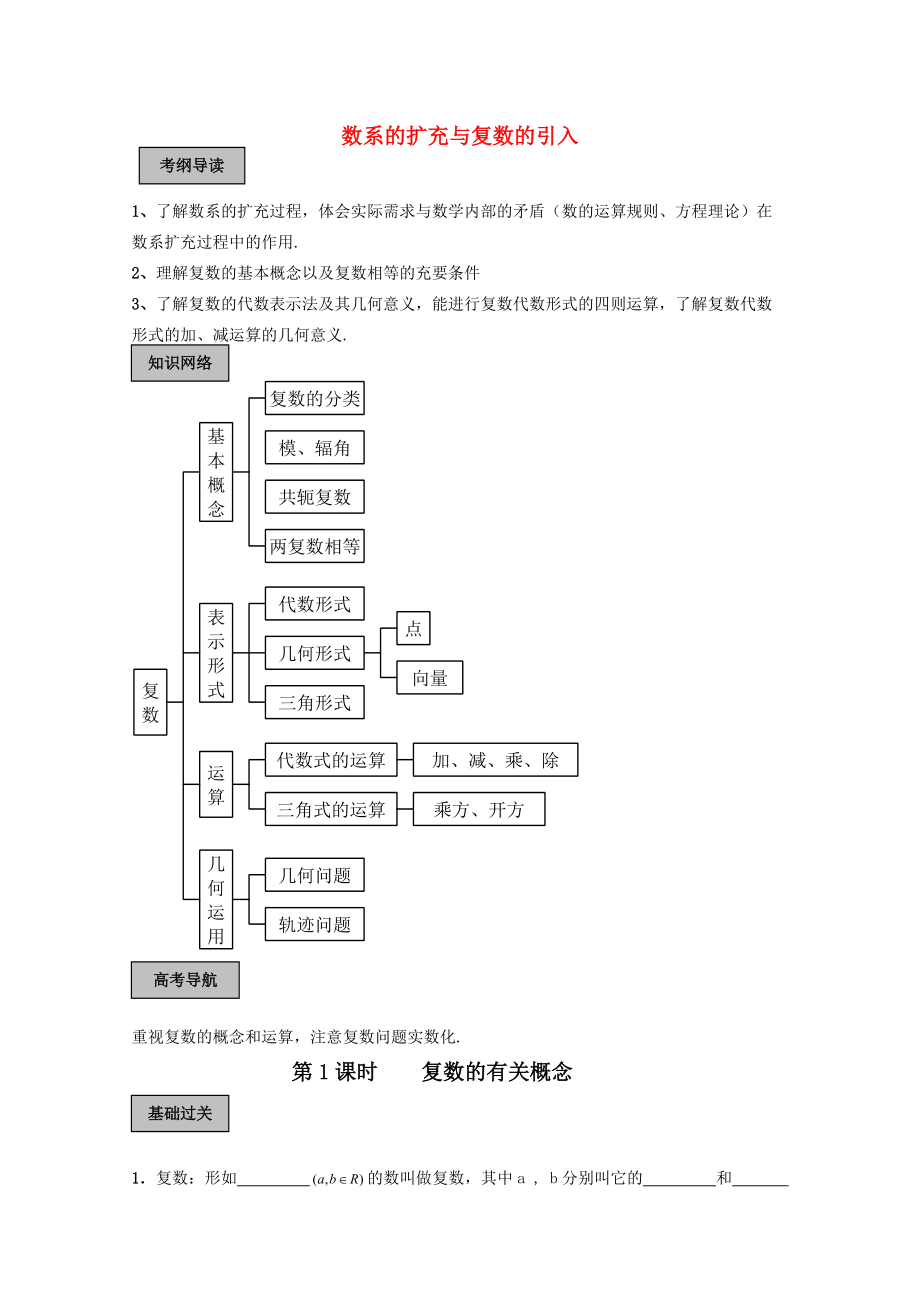
1�����、考綱導(dǎo)讀數(shù)系的擴(kuò)充與復(fù)數(shù)的引入1���、了解數(shù)系的擴(kuò)充過(guò)程,體會(huì)實(shí)際需求與數(shù)學(xué)內(nèi)部的矛盾(數(shù)的運(yùn)算規(guī)則����、方程理論)在數(shù)系擴(kuò)充過(guò)程中的作用.2、理解復(fù)數(shù)的基本概念以及復(fù)數(shù)相等的充要條件3�����、了解復(fù)數(shù)的代數(shù)表示法及其幾何意義�����,能進(jìn)行復(fù)數(shù)代數(shù)形式的四則運(yùn)算�,了解復(fù)數(shù)代數(shù)形式的加、減運(yùn)算的幾何意義.知識(shí)網(wǎng)絡(luò)高考導(dǎo)航重視復(fù)數(shù)的概念和運(yùn)算��,注意復(fù)數(shù)問(wèn)題實(shí)數(shù)化.第1課時(shí) 復(fù)數(shù)的有關(guān)概念基礎(chǔ)過(guò)關(guān)1復(fù)數(shù):形如 的數(shù)叫做復(fù)數(shù)���,其中a , b分別叫它的 和 2分類(lèi):設(shè)復(fù)數(shù):(1) 當(dāng) 0時(shí)�����,z為實(shí)數(shù)�����;(2) 當(dāng) 0時(shí)��,z為虛數(shù)�;(3) 當(dāng) 0, 且 0時(shí),z為純虛數(shù).3復(fù)數(shù)相等:如果兩個(gè)復(fù)數(shù) 相等且 相等就說(shuō)這兩個(gè)復(fù)數(shù)相等
2��、.4共軛復(fù)數(shù):當(dāng)兩個(gè)復(fù)數(shù)實(shí)部 ��,虛部 時(shí)這兩個(gè)復(fù)數(shù)互為共軛復(fù)數(shù)(當(dāng)虛部不為零時(shí)�,也可說(shuō)成互為共軛虛數(shù))5若zabi, (a, bR), 則 | z | ����; z .6復(fù)平面:建立直角坐標(biāo)系來(lái)表示復(fù)數(shù)的平面叫做復(fù)平面, x軸叫做 , 叫虛軸7復(fù)數(shù)zabi(a, bR)與復(fù)平面上的點(diǎn) 建立了一一對(duì)應(yīng)的關(guān)系8兩個(gè)實(shí)數(shù)可以比較大小�����、但兩個(gè)復(fù)數(shù)如果不全是實(shí)數(shù)����,就 比較它們的大小.典型例題例1. m取何實(shí)數(shù)值時(shí)���,復(fù)數(shù)z是實(shí)數(shù)?是純虛數(shù)��?解: z是實(shí)數(shù) z為純虛數(shù)變式訓(xùn)練1:當(dāng)m分別為何實(shí)數(shù)時(shí)��,復(fù)數(shù)z=m21(m23m2)i是(1)實(shí)數(shù)�?(2)虛數(shù)?(3)純虛數(shù)���?(4)零��?解:(1)m=1,m=2����;(2)m1
3����、,m2;(3)m=1�;(4)m=1例2. 已知x、y為共軛復(fù)數(shù)���,且�,求x解:設(shè)代入由復(fù)數(shù)相等的概念可得變式訓(xùn)練2:已知復(fù)數(shù)z=1i,如果=1i,求實(shí)數(shù)a,b的值由z=1i得=(a2)(ab)i從而���,解得例3. 若方程至少有一個(gè)實(shí)根����,試求實(shí)數(shù)m的值.解:設(shè)實(shí)根為�,代入利用復(fù)數(shù)相等的概念可得變式訓(xùn)練3:若關(guān)于x 的方程x2(t23ttx )i=0有純虛數(shù)根,求實(shí)數(shù)t的值和該方程的根解:t=3,x1=0,x2=3i提示:提示:設(shè)出方程的純虛數(shù)根���,分別令實(shí)部��、虛部為0,將問(wèn)題轉(zhuǎn)化成解方程組例4. 復(fù)數(shù)滿(mǎn)足��,試求的最小值.設(shè)��,則���,于是變式訓(xùn)練4:已知復(fù)平面內(nèi)的點(diǎn)A����、B對(duì)應(yīng)的復(fù)數(shù)分別是、�,其中,設(shè)對(duì)應(yīng)的復(fù)
4��、數(shù)為.(1) 求復(fù)數(shù)�����;(2) 若復(fù)數(shù)對(duì)應(yīng)的點(diǎn)P在直線上�,求的值.解:(1) (2) 將代入可得.小結(jié)歸納1要理解和掌握復(fù)數(shù)為實(shí)數(shù)、虛數(shù)���、純虛數(shù)���、零時(shí),對(duì)實(shí)部和虛部的約束條件.2設(shè)zabi (a����,bR),利用復(fù)數(shù)相等和有關(guān)性質(zhì)將復(fù)數(shù)問(wèn)題實(shí)數(shù)化是解決復(fù)數(shù)問(wèn)題的常用方法.第2課時(shí) 復(fù)數(shù)的代數(shù)形式及其運(yùn)算基礎(chǔ)過(guò)關(guān)1復(fù)數(shù)的加�、減、乘����、除運(yùn)算按以下法則進(jìn)行:設(shè)�,則(1) �;(2) ;(3) ( ).2幾個(gè)重要的結(jié)論: . 若z為虛數(shù)����,則 3運(yùn)算律 . . .典型例題例1計(jì)算:解:提示:利用原式0變式訓(xùn)練1:求復(fù)數(shù)(A) (B) (C) (D)解: 故選C;例2. 若���,求解:提示:利用原式變式訓(xùn)練2:已知復(fù)
5���、數(shù)z滿(mǎn)足z210,則(z6i)(z6i) 解:2例3. 已知���,問(wèn)是否存在復(fù)數(shù)z�����,使其滿(mǎn)足(aR),如果存在���,求出z的值���,如果不存在���,說(shuō)明理由解:提示:設(shè)利用復(fù)數(shù)相等的概念有變式訓(xùn)練3:若,其中是虛數(shù)單位�,則ab_解:3例4. 證明:在復(fù)數(shù)范圍內(nèi),方程(為虛數(shù)單位)無(wú)解證明:原方程化簡(jiǎn)為設(shè) �、yR,代入上述方程得 將(2)代入(1)��,整理得無(wú)實(shí)數(shù)解����,原方程在復(fù)數(shù)范圍內(nèi)無(wú)解.變式訓(xùn)練4:已知復(fù)數(shù)z1滿(mǎn)足(1i)z115i,z2a2i��,其中i為虛數(shù)單位����,aR, 若,求a的取值范圍.解:由題意得 z123i,于是=,=.小結(jié)歸納 由����,得a28a70,1a0)��,且復(fù)數(shù)的虛部減去它的實(shí)部所得的差等于,求復(fù)
6�、數(shù)的模.20復(fù)平面內(nèi),點(diǎn)��、分別對(duì)應(yīng)復(fù)數(shù)���、��,且�,若可以與任意實(shí)數(shù)比較大小����,求的值(O為坐標(biāo)原點(diǎn)).復(fù)數(shù)章節(jié)測(cè)試題答案一、選擇題1 A 2答案:A 3答案:B4答案:B6答案:A7A8B9B10B11D12B二�����、填空題13 142i1516答案:17答案:18 答案:B , 設(shè)k =,則k為過(guò)圓(x2)2 + y2 = 1上點(diǎn)及原點(diǎn)82615205的直線斜率��,作圖如下, k, 又y0 ,k0.由對(duì)稱(chēng)性 選B【幫你歸納】本題考查復(fù)數(shù)的概念,以及轉(zhuǎn)化與化歸的數(shù)學(xué)思維能力�,利用復(fù)數(shù)與解析幾何、平面幾何之間的關(guān)系求解.虛數(shù)一詞又強(qiáng)調(diào)y0���,這一易錯(cuò)點(diǎn).【誤區(qū)警示】本題屬于基礎(chǔ)題,每步細(xì)心計(jì)算是求解本題的關(guān)鍵,否則將會(huì)遭遇“千里之堤��,潰于蟻穴”之尷尬.19解:20解:依題意為實(shí)數(shù)��,可得
 2010高考數(shù)學(xué)導(dǎo)學(xué)練系列 復(fù)數(shù)教案 蘇教版
2010高考數(shù)學(xué)導(dǎo)學(xué)練系列 復(fù)數(shù)教案 蘇教版