高三數(shù)學(xué)北師大版理一輪教師用書：第4章 第5節(jié) 第2課時(shí) 簡單的三角恒等變換 Word版含解析

《高三數(shù)學(xué)北師大版理一輪教師用書：第4章 第5節(jié) 第2課時(shí) 簡單的三角恒等變換 Word版含解析》由會(huì)員分享，可在線閱讀，更多相關(guān)《高三數(shù)學(xué)北師大版理一輪教師用書：第4章 第5節(jié) 第2課時(shí) 簡單的三角恒等變換 Word版含解析（9頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

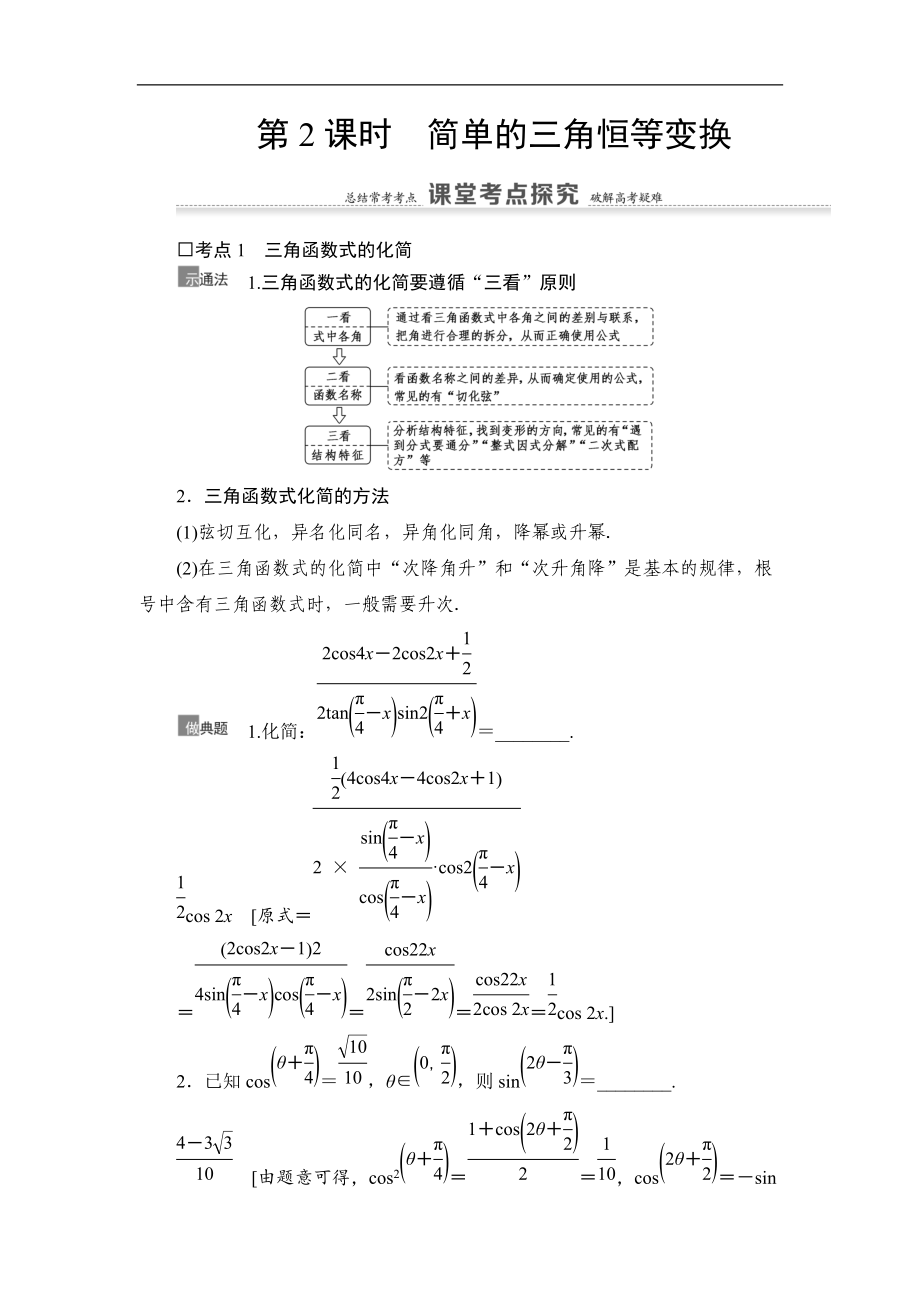
1、 第2課時(shí)　簡單的三角恒等變換 考點(diǎn)1　三角函數(shù)式的化簡 　1.三角函數(shù)式的化簡要遵循“三看”原則 2．三角函數(shù)式化簡的方法 (1)弦切互化，異名化同名，異角化同角，降冪或升冪． (2)在三角函數(shù)式的化簡中“次降角升”和“次升角降”是基本的規(guī)律，根號中含有三角函數(shù)式時(shí)，一般需要升次． 　1.化簡：＝________. cos 2x　[原式＝ ＝＝＝＝cos 2x.] 2．已知cos＝，θ∈，則sin＝________. 　[由題意可得，cos2＝＝，cos＝－sin 2θ＝－，即sin 2θ＝. 因?yàn)閏os＝＞0，θ∈， 所以0＜θ＜，2θ∈， 根據(jù)同角三

2、角函數(shù)基本關(guān)系式，可得cos 2θ＝， 由兩角差的正弦公式，可得 sin＝sin 2θcos －cos 2θsin ＝×－×＝.] 3．已知α為第二象限角，且tan α＋tan ＝2tan αtan －2，則sin＝________. －　[由已知可得tan＝－2， ∵α為第二象限角， ∴sin＝，cos＝－， 則sin＝－sin＝－sin ＝cossin －sincos ＝－.] 　(1)化簡標(biāo)準(zhǔn)：函數(shù)種類盡可能少、次數(shù)盡可能低、項(xiàng)數(shù)盡可能少、盡量不含根式、盡量不含絕對值等． (2)余弦的二倍角公式、正弦的二倍角公式都能起到升(降)冪的作用． 考點(diǎn)2　三角函數(shù)的求

3、值 　給角求值 　[2sin 50°＋sin 10°(1＋tan 10°)]·＝________. 　[原式＝·sin 80°＝·cos 10°＝2[sin 50°·cos 10°＋sin 10°·cos(60°－10°)]＝2sin(50°＋10°)＝2×＝.] 　該類問題中給出的角一般都不是特殊角，需要通過三角恒等變換將其變?yōu)樘厥饨牵蛘吣軌蛘?fù)相消，或者能夠約分相消，最后得到具體的值． 　給值求值 　(1)(2019·益陽模擬)已知cos＋sin α＝，則sin＝________. (2)已知cos＝，＜α＜，則的值為________． (1)－　(2)－　[(1)由co

4、s＋sin α＝， 可得cos α＋ sin α＋sin α＝， 即sin α＋cos α＝， 所以sin＝，即sin＝， 所以sin＝－sin＝－. (2)＝ ＝ ＝sin 2α＝sin 2α·tan. 由＜α＜得＜α＋＜2π， 又cos＝， 所以sin＝－，tan＝－. cos α＝cos＝－，sin α＝－， sin 2α＝. 所以＝×＝－.] 　(1)給值求值的關(guān)鍵是通過角的三角函數(shù)的變換把求解目標(biāo)用已知條件表達(dá)出來． (2)注意與互余，sin 2＝cos 2x，cos 2＝sin 2x的靈活應(yīng)用． 　給值求角 　(1)設(shè)α，β為鈍角，且sin α＝，

5、cos β＝－，則α＋β的值為(　　) A.　 B. C. D.或 (2)已知α，β∈(0，π)，且tan(α－β)＝，tan β＝－，則2α－β的值為________． (1)C　(2)－π　[(1)∵α，β為鈍角，sin α＝，cos β＝－， ∴cos α＝－，sin β＝， ∴cos(α＋β)＝cos αcos β－sin αsin β＝＞0. 又α＋β∈(π，2π)，∴α＋β∈， ∴α＋β＝. (2)∵tan α＝tan[(α－β)＋β] ＝＝＝＞0， ∴0＜α＜. 又∵tan 2α＝＝＝＞0， ∴0＜2α＜， ∴tan(2α－β)＝＝＝1. ∵tan

6、β＝－＜0，∴＜β＜π，－π＜2α－β＜0， ∴2α－β＝－.] 　通過求角的某種三角函數(shù)值來求角，在選取函數(shù)時(shí)，有以下原則： (1)已知正切函數(shù)值，則選正切函數(shù)． (2)已知正、余弦函數(shù)值，則選正弦或余弦函數(shù)．若角的范圍是，則選正、余弦皆可；若角的范圍是(0，π)，則選余弦較好；若角的范圍為，則選正弦較好． 提醒：求解此類問題時(shí)，一定要注意所求角的范圍及解題過程中角的范圍． 　1.(2019·安徽六安二模)若sin 2α＝，sin(β－α)＝，且α∈，β∈，則α＋β的值是(　　) A. B. C.或 D.或 A　[因?yàn)棣痢剩?＜sin 2α＝＜，所以2α∈， 所以α∈

7、，cos 2α＝－＝－. 因?yàn)棣隆剩? 所以β－α∈， 又sin(β－α)＝＞0， 所以β－α∈， 所以cos(β－α)＝－＝－. 所以cos(α＋β)＝cos[2α＋(β－α)] ＝cos 2αcos(β－α)－sin 2αsin(β－α) ＝－×－×＝. 又α∈，β∈， 所以α＋β∈， 所以α＋β＝.故選A.] 2．已知α∈，且2sin2α－sin α·cos α－3cos2α＝0，則＝________. 　[∵α∈，且2sin2α－sin α·cos α－3cos2α＝0， 則(2sin α－3cos α)·(sin α＋cos α)＝0， 又∵α∈，sin

8、α＋cos α＞0， ∴2sin α＝3cos α， 又sin2α＋cos2α＝1， ∴cos α＝，sin α＝， ∴ ＝＝＝.] 考點(diǎn)3　三角恒等變換的綜合應(yīng)用 　三角恒等變換的應(yīng)用策略 (1)進(jìn)行三角恒等變換要抓?。鹤兘?、變函數(shù)名稱、變結(jié)構(gòu)，尤其是角之間的關(guān)系；注意公式的逆用和變形使用． (2)把形如y＝asin x＋bcos x化為y＝sin(x＋φ)，可進(jìn)一步研究函數(shù)的周期性、單調(diào)性、最值與對稱性． 　(2019·浙江高考)設(shè)函數(shù)f(x)＝sin x，x∈R. (1)已知θ∈[0,2π)，函數(shù)f(x＋θ)是偶函數(shù)，求θ的值； (2)求函數(shù)y＝2＋2的值域．

9、 [解]　(1)因?yàn)閒(x＋θ)＝sin(x＋θ)是偶函數(shù)， 所以對任意實(shí)數(shù)x都有sin(x＋θ)＝sin(－x＋θ)， 即sin xcos θ＋cos xsin θ＝－sin xcos θ＋cos xsin θ， 故2sin xcos θ＝0，所以cos θ＝0. 又θ∈[0,2π)，因此θ＝或θ＝. (2)y＝2＋2 ＝sin2＋sin2＝＋ ＝1－＝1－cos. 因此，所求函數(shù)的值域是. 　(1)求三角函數(shù)解析式y(tǒng)＝Asin(ωx＋φ)(A＞0，ω＞0)時(shí)要注意φ的取值范圍．(2)根據(jù)二倍角公式進(jìn)行計(jì)算時(shí)，如果涉及開方，則要注意開方后三角函數(shù)值的符號． 　已知函數(shù)f(x)＝sin2x－cos2x－2sin xcos x(x∈R)． (1)求f 的值； (2)求f(x)的最小正周期及單調(diào)遞增區(qū)間． [解]　(1)由sin＝，cos ＝－，得 f ＝2－2－2××＝2. (2)由cos 2x＝cos2x－sin2x與sin 2x＝2sin xcos x， 得f(x)＝－cos 2x－sin 2x＝－2sin. 所以f(x)的最小正周期是π. 由正弦函數(shù)的性質(zhì)，得 ＋2kπ≤2x＋≤＋2kπ，k∈Z， 解得＋kπ≤x≤＋kπ，k∈Z. 所以f(x)的單調(diào)遞增區(qū)間為 (k∈Z).