人教版八年級(jí)上冊(cè)數(shù)學(xué) 第11章 三角形 單元練習(xí)試題

《人教版八年級(jí)上冊(cè)數(shù)學(xué) 第11章 三角形 單元練習(xí)試題》由會(huì)員分享，可在線閱讀，更多相關(guān)《人教版八年級(jí)上冊(cè)數(shù)學(xué) 第11章 三角形 單元練習(xí)試題（9頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

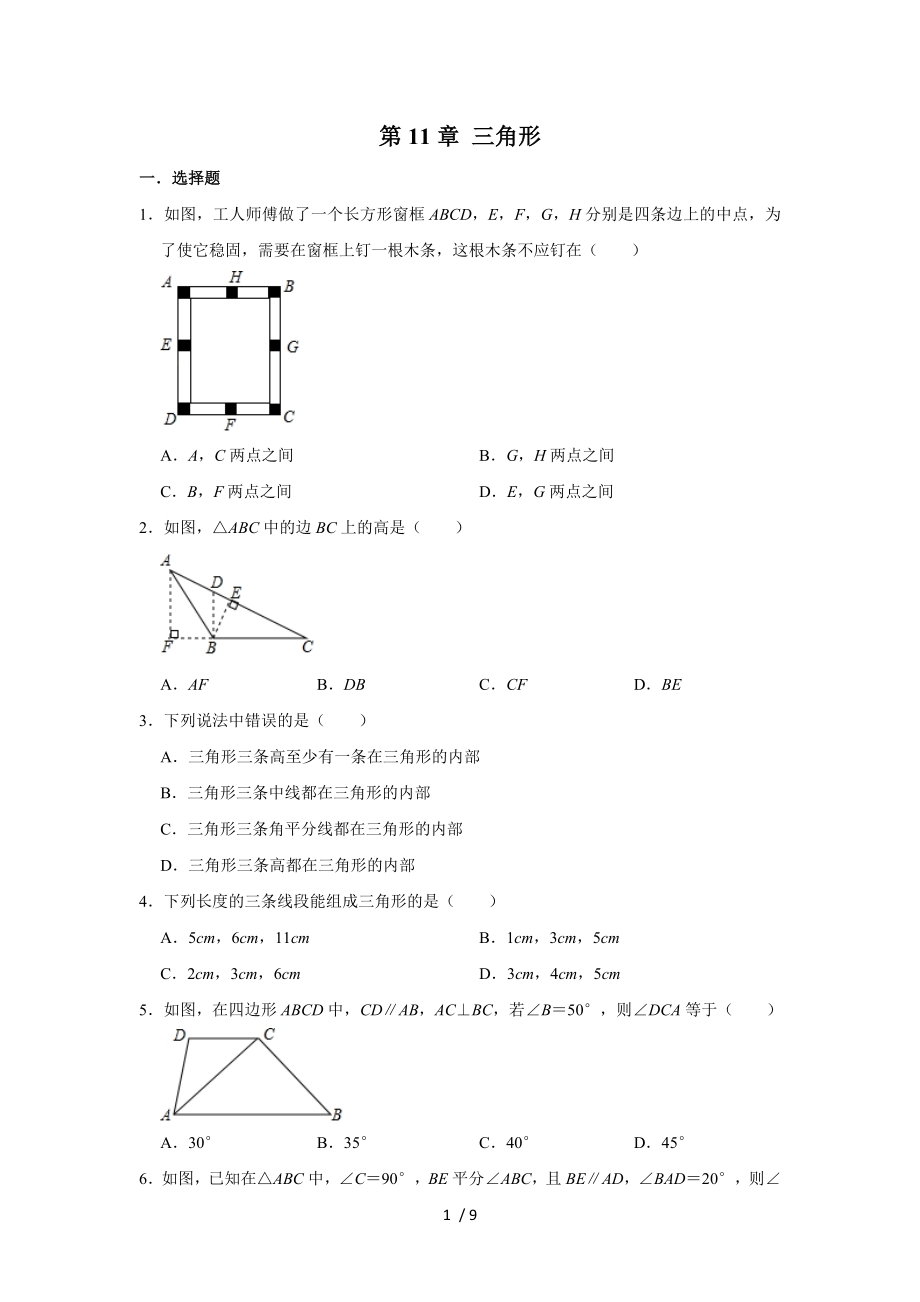
1、第11章 三角形 一．選擇題 1．如圖，工人師傅做了一個(gè)長(zhǎng)方形窗框ABCD，E，F(xiàn)，G，H分別是四條邊上的中點(diǎn)，為了使它穩(wěn)固，需要在窗框上釘一根木條，這根木條不應(yīng)釘在（　?。? A．A，C兩點(diǎn)之間 B．G，H兩點(diǎn)之間 C．B，F(xiàn)兩點(diǎn)之間 D．E，G兩點(diǎn)之間 2．如圖，△ABC中的邊BC上的高是（　?。? A．AF B．DB C．CF D．BE 3．下列說(shuō)法中錯(cuò)誤的是（　　） A．三角形三條高至少有一條在三角形的內(nèi)部 B．三角形三條中線都在三角形的內(nèi)部 C．三角形三條角平分線都在三角形的內(nèi)部 D．三角形三條高都在三角形的內(nèi)部 4．下列長(zhǎng)度的三條線段能組成三角形

2、的是（　?。? A．5cm，6cm，11cm B．1cm，3cm，5cm C．2cm，3cm，6cm D．3cm，4cm，5cm 5．如圖，在四邊形ABCD中，CD∥AB，AC⊥BC，若∠B＝50°，則∠DCA等于（　?。? A．30° B．35° C．40° D．45° 6．如圖，已知在△ABC中，∠C＝90°，BE平分∠ABC，且BE∥AD，∠BAD＝20°，則∠AEB的度數(shù)為（　　） A．100° B．110° C．120° D．130° 7．如圖，已知∠BED＝55°，則∠B+∠C＝（　　） A．30° B．35° C．45° D．55° 8．如圖，∠1是五

3、邊形ABCDE的一個(gè)外角．若∠1＝70°，則∠A+∠B+∠C+∠D等于（　?。? A．610° B．470° C．290° D．430° 9．如圖，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足為D，AF平分∠CAB，交CD于點(diǎn)E，交CB于點(diǎn)F，則下列結(jié)論成立的是（　　） A．EC＝EF B．FE＝FC C．CE＝CF D．CE＝CF＝EF 10．如圖，點(diǎn)D在△ABC內(nèi)，且∠BDC＝120°，∠1+∠2＝55°，則∠A的度數(shù)為（　　） A．50° B．60° C．65° D．75° 二．填空題 11．若三角形有兩邊長(zhǎng)分別為2和5，第三邊為a，則a的取值范圍是　

4、 ?。? 12．如圖，在Rt△ABC中，∠C＝90°，CD⊥AB，垂足為D．若∠A＝32°，則∠BCD＝　 　°． 13．在Rt△ABC中，CD是斜邊AB上的高，∠A＝25°，則∠B＝　 　，∠BCD＝　 ?。? 14．如果直角三角形的一個(gè)內(nèi)角為40°，則這個(gè)直角三角形的另一個(gè)銳角為　 ?。? 15．如圖，在四邊形ABCD中，AB∥CD，∠BAD、∠ADC的平分線AE、DF分別與線段BC相交于點(diǎn)E、F，∠DFC＝30°，AE與DF相交于點(diǎn)G，則∠AEC＝　 ?。? 三．解答題 16．如圖，△ABC的周長(zhǎng)是21cm，AB＝AC，中線BD分△ABC為兩個(gè)三角形，且△

5、ABD的周長(zhǎng)比△BCD的周長(zhǎng)大6cm，求AB，BC． 17．如圖，在△ABC中、D、E分別是AB，BC上任意一點(diǎn)，連結(jié)DE，若BD＝4，DE＝5． （1）BE的取值范圍　 ?。? （2）若DE∥AC，∠A＝85°，∠BED＝35°，求∠B的度數(shù)． 18．如圖，已知△ABC中，∠BAC＝70°，∠B＝30°，點(diǎn)F是AB上一點(diǎn)，且∠BCF＝25°，點(diǎn)D在邊CA的延長(zhǎng)線上，AE平分∠BAD，說(shuō)明CF∥AE的理由． 解：因?yàn)辄c(diǎn)D在邊CA的延長(zhǎng)線上（已知）， 所以∠BAC+∠BAD＝180°（　 ?。? 因?yàn)椤螧AC＝70°（已知）， 所以∠BAD＝180°﹣∠BAC＝11

6、0°（等式性質(zhì)）． 因?yàn)锳E平分∠BAD（已知）， 所以∠EAB＝∠BAD＝55°（　 ?。? 因?yàn)椤螦FC＝　 　+　 ?。?5°（　 ?。?， 所以　 ?。健? 　（等量代換）． 所以CF∥AE（　 ?。? 19．如圖1，在△ABC中，∠A＝60°，∠CBM，∠BCN是△ABC的外角，∠CBM，∠BCN的平分線BD，CD交于點(diǎn)D． （1）求∠BDC的度數(shù)； （2）在圖1中，過(guò)點(diǎn)D作DE⊥BD，垂足為點(diǎn)D，過(guò)點(diǎn)B作BF∥DE交DC的延長(zhǎng)線于點(diǎn)F（如圖2），求證：BF是∠ABC的平分線． 20．如圖，四邊形ABCD，BE、DF分別平分四邊形的外

7、角∠MBC和∠NDC，若∠BAD＝α，∠BCD＝β． （1）如圖1，若α+β＝100°，求∠MBC+∠NDC的度數(shù)； （2）如圖1，若BE與DF相交于點(diǎn)G，∠BGD＝40°，請(qǐng)直接寫(xiě)出α、β所滿足的數(shù)量關(guān)系式； （3）如圖2，若α＝β，判斷BE、DF的位置關(guān)系，并說(shuō)明理由． 參考答案 一．選擇題 1． D． 2．A． 3．D． 4． D． 5． C． 6． B． 7．D． 8． D． 9． C． 10． C． 二．填空題 11． 3＜a＜7． 12． 32． 13． 65°、25°． 14． 50° 15． 120°． 三．解答題 1

8、6．解：∵BD是中線， ∴AD＝CD＝AC， ∵△ABD的周長(zhǎng)比△BCD的周長(zhǎng)大6cm， ∴（AB+AD+BD）﹣（BD+CD+BC）＝AB﹣BC＝6cm①， ∵△ABC的周長(zhǎng)是21cm，AB＝AC， ∴2AB+BC＝21cm②， 聯(lián)立①②得：AB＝9cm，BC＝3cm． 17．解：（1）∵BD＝4，DE＝5， ∴△BDE中，5﹣4＜BE＜5+4， 即1＜BE＜9， 即BE的取值范圍為：1＜BE＜9； 故答案為：1＜BE＜9； （2）∵DE∥AC， ∴∠BED＝∠C＝35°， 又∵∠A＝85°， ∴△ABC中，∠B＝180°﹣∠A﹣∠C＝180°﹣85°﹣35°＝

9、60°． 18．解：∵點(diǎn)D在邊CA的延長(zhǎng)線上（已知）， ∴∠BAC+∠BAD＝180（鄰補(bǔ)角定義）， ∵∠BAC＝70°（已知）， ∴∠BAD＝180°﹣∠BAC＝110°（等式性質(zhì)）． ∵AE平分∠BAD（已知）， ∴∠EAB＝∠EAB＝∠BAD＝55°（角平分線定義）， ∵∠AFC＝∠B+∠BCF＝55°（三角形的一個(gè)外角等于和它不相鄰的兩個(gè)內(nèi)角的和）， ∴∠AFC＝∠EAB（等量代換）， ∴CF∥AE（內(nèi)錯(cuò)角相等，兩直線平行）， 故答案為：鄰補(bǔ)角定義，角平分線定義，∠B，∠BCF，三角形的一個(gè)外角等于和它不相鄰的兩個(gè)內(nèi)角的和，∠AFC，∠EAB，內(nèi)錯(cuò)角相等，兩直線平行

10、． 19．解：（1）∵△ABC中，∠A＝60°， ∴∠ABC+∠ACB＝120°， 又∵∠ABM＝∠ACN＝180°， ∴∠CBM+∠BCN＝360°﹣120°＝240°， 又∵∠CBM，∠BCN的平分線BD，CD交于點(diǎn)D， ∴∠CBD＝∠CBM，∠BCD＝∠BCN， ∴△BCD中，∠DBC+∠BCD＝（∠CBM+∠BCN）＝×240°＝120°， ∴∠D＝180°﹣120°＝60°； （2）如圖2，∵DE⊥BD，BF∥DE， ∴∠DBF＝180°﹣90°＝90°， 即∠2+∠3＝90°， ∴∠1+∠4＝90°， 又∵∠3＝∠4， ∴∠1＝∠2， ∴BF是∠A

11、BC的平分線． 20．解：（1）∵∠ABC+∠ADC＝360°﹣（α+β）， ∴∠MBC+∠NDC＝180°﹣∠ABC+180°﹣∠ADC＝α+β＝100°． （2）β﹣α＝80° 理由：如圖1，連接BD， 由（1）有，∠MBC+∠NDC＝α+β， ∵BE、DF分別平分四邊形的外角∠MBC和∠NDC， ∴∠CBG＝∠MBC，∠CDG＝∠NDC， ∴∠CBG+∠CDG＝∠MBC+∠NDC＝（∠MBC+∠NDC）＝（α+β）， 在△BCD中，∠BDC+∠CBD＝180°﹣∠BCD＝180°﹣β， 在△BDG中，∠GBD+∠GDB+∠BGD＝180°， ∴∠CBG+∠C

12、BD+∠CDG+∠BDC+∠BGD＝180°， ∴（∠CBG+∠CDG）+（∠BDC+∠CBD）+∠BGD＝180°， ∴（α+β）+180°﹣β+40°＝180°， ∴β﹣α＝80°， （3）平行， 理由：如圖2，延長(zhǎng)BC交DF于H， 由（1）有，∠MBC+∠NDC＝α+β， ∵BE、DF分別平分四邊形的外角∠MBC和∠NDC， ∴∠CBE＝∠MBC，∠CDH＝∠NDC， ∴∠CBE+∠CDH＝∠MBC+∠NDC＝（∠MBC+∠NDC）＝（α+β）， ∵∠BCD＝∠CDH+∠DHB， ∴∠CDH＝∠BCD﹣∠DHB＝β﹣∠DHB， ∴∠CBE+β﹣∠DHB＝（α+β）， ∵α＝β， ∴∠CBE+β﹣∠DHB＝（β+β）＝β， ∴∠CBE＝∠DHB， ∴BE∥DF． 9 / 9