（安徽專版）2018年秋九年級(jí)數(shù)學(xué)下冊(cè) 復(fù)習(xí)自測(cè)9 圓(B)習(xí)題 （新版）滬科版

《（安徽專版）2018年秋九年級(jí)數(shù)學(xué)下冊(cè) 復(fù)習(xí)自測(cè)9 圓(B)習(xí)題 （新版）滬科版》由會(huì)員分享，可在線閱讀，更多相關(guān)《（安徽專版）2018年秋九年級(jí)數(shù)學(xué)下冊(cè) 復(fù)習(xí)自測(cè)9 圓(B)習(xí)題 （新版）滬科版（7頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

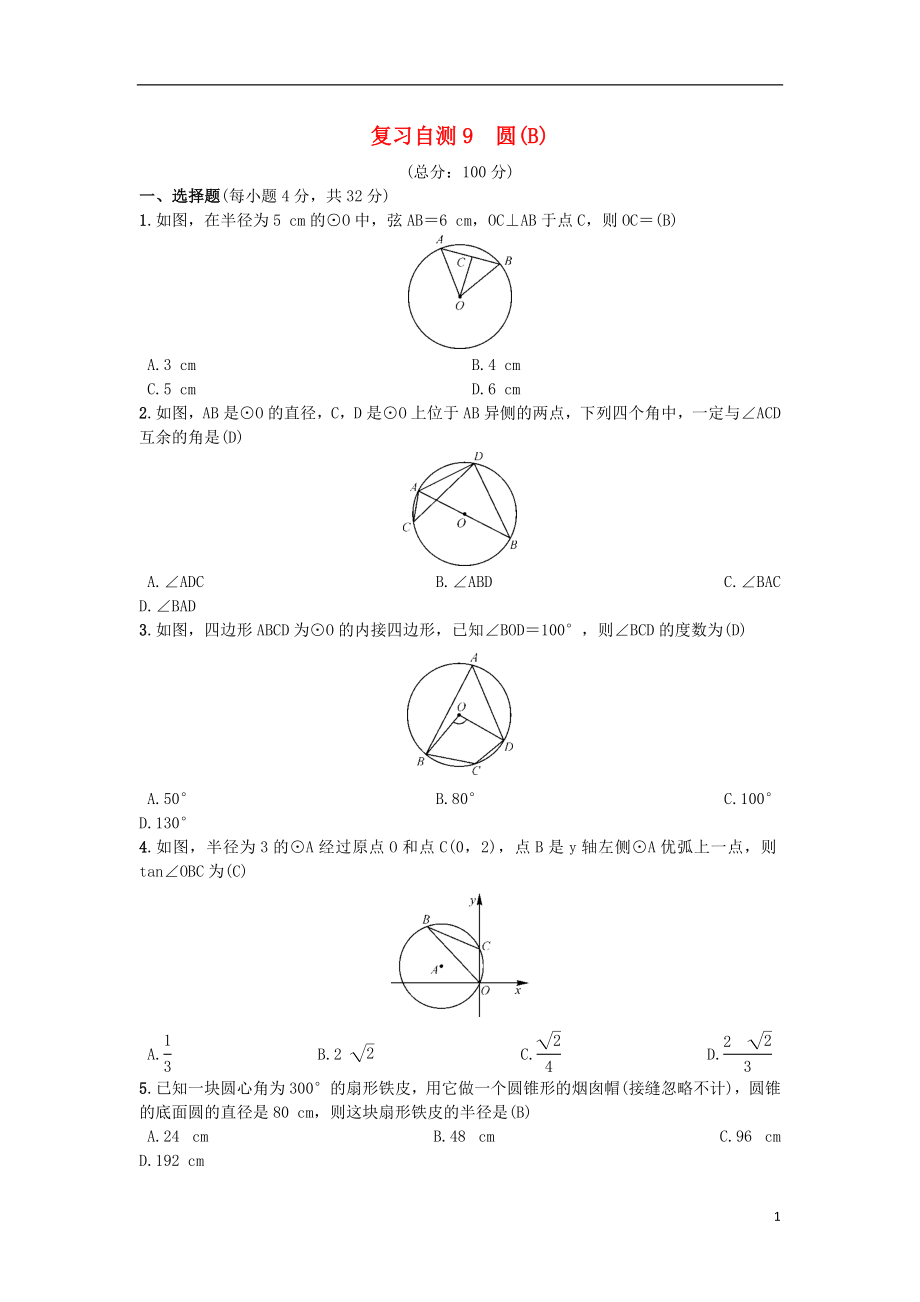
1、 復(fù)習(xí)自測(cè)9　圓(B) (總分：100分)　　　　　　　　　　　　 一、選擇題(每小題4分，共32分) 1.如圖，在半徑為5 cm的⊙O中，弦AB＝6 cm，OC⊥AB于點(diǎn)C，則OC＝(B) A.3 cm B.4 cm C.5 cm D.6 cm 2.如圖，AB是⊙O的直徑，C，D是⊙O上位于AB異側(cè)的兩點(diǎn)，下列四個(gè)角中，一定與∠ACD互余的角是(D) A.∠ADC B.∠ABD

2、 C.∠BAC D.∠BAD 3.如圖，四邊形ABCD為⊙O的內(nèi)接四邊形，已知∠BOD＝100°，則∠BCD的度數(shù)為(D) A.50° B.80° C.100° D.130° 4.如圖，半徑為3的⊙A經(jīng)過(guò)原點(diǎn)O和點(diǎn)C(0，2)，點(diǎn)B是y軸左側(cè)⊙A優(yōu)弧上一點(diǎn)，則tan∠OBC為(C) A. B.2 C. D. 5.已知一塊圓心角為3

3、00°的扇形鐵皮，用它做一個(gè)圓錐形的煙囪帽(接縫忽略不計(jì))，圓錐的底面圓的直徑是80 cm，則這塊扇形鐵皮的半徑是(B) A.24 cm B.48 cm C.96 cm D.192 cm 6.如圖，PA和PB是⊙O的切線，點(diǎn)A，B是切點(diǎn)，AC是⊙O的直徑，已知∠P＝40°，則∠ACB的大小是(C) A.60° B.65° C.70° D.75° 7.如圖，⊙O的半徑為3，四邊形ABCD

4、內(nèi)接于⊙O，連接OB，OD.若∠BOD＝∠BCD，則劣弧的長(zhǎng)為(C) A.π B.π C.2π D.3π 8.如圖，將矩形ABCD繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)90°至矩形AEFG，點(diǎn)D的旋轉(zhuǎn)路徑為.若AB＝1，BC＝2，則陰影部分的面積為(A) A.＋ B.1＋ C. D.＋1 二、填空題(

5、每小題4分，共24分) 9.如圖，一塊含有45°角的直角三角板，它的一個(gè)銳角頂點(diǎn)A在⊙O上，邊AB，AC分別與⊙O交于點(diǎn)D，E，則∠DOE的度數(shù)為90°. 10.已知△ABC在網(wǎng)格中的位置如圖，那么△ABC對(duì)應(yīng)的外接圓的圓心坐標(biāo)是(2，0). 11.如圖，⊙O是△ABC的外接圓，直徑AD＝4，∠ABC＝∠DAC，則AC長(zhǎng)為2__. 12.如圖，正方形ABCD內(nèi)接于⊙O，其邊長(zhǎng)為4，則⊙O的內(nèi)接正三角形EFG的邊長(zhǎng)為2. 13.如圖，直線AB與半徑為2的⊙O相切于點(diǎn)C，點(diǎn)D是⊙O上一點(diǎn)，且∠EDC＝30°，弦EF∥AB，則EF的長(zhǎng)度為2__. 14.在半徑為1的⊙

6、O中，弦AB，AC的長(zhǎng)分別為1和 ，則∠BAC的度數(shù)為105°或15°. 三、解答題(共44分) 15.(8分)如圖，在⊙O中，直徑AB⊥CD于點(diǎn)E，連接CO并延長(zhǎng)交AD于點(diǎn)F，且CF⊥AD.求∠D的度數(shù). 解：∵在⊙O中，D為圓上一點(diǎn)， ∴∠AOC＝2∠D. ∴∠EOF＝∠AOC＝2∠D. ∵在四邊形FOED中， ∠CFD＋∠D＋∠DEO＋∠EOF＝360°， ∴90°＋∠D＋90°＋2∠D＝360°. ∴∠D＝60°. 16.(10分)如圖，在△ABC中，以AC為直徑的⊙O分別交AB，BC于點(diǎn)D，E，連接DE，AD＝BD，∠ADE＝120°. (1

7、)試判斷△ABC的形狀，并說(shuō)明理由； (2)若AC＝2，求圖中陰影部分的面積. 解：(1)△ABC是等邊三角形. 理由：連接CD. ∵AC為⊙O的直徑， ∴CD⊥AB. ∵AD＝BD，∴AC＝BC. ∵四邊形ADEC為內(nèi)接四邊形， ∴∠ADE＋∠ACE＝180°. ∵∠ADE＝120°，∴∠ACE＝60°. ∴△ABC是等邊三角形. (2)∵△ABC是等邊三角形， ∴∠A＝∠ACB＝∠B＝60°. ∵∠ADE＝120°，∴∠BDE＝60°. ∴∠BED＝∠BDE＝∠B＝60°. ∴△BDE是等邊三角形. ∴BD＝ED. ∵AD＝BD，∴DE＝AD.∴＝.

8、 ∴S弓形DE＝S弓形AD.∴S陰影＝S△DEB. ∵AC＝2，∴BD＝1. ∴S陰影＝S△DEB＝×1×＝. 17.(12分)如圖，已知A，B，C是⊙O上的三個(gè)點(diǎn)，四邊形OABC是平行四邊形，過(guò)點(diǎn)C作⊙O的切線，交AB的延長(zhǎng)線于點(diǎn)D. (1)求∠ADC的大?。? (2)經(jīng)過(guò)點(diǎn)O作CD的平行線，與AB交于點(diǎn)E，與交于點(diǎn)F，連接AF，求∠FAB的大小. 解：(1)∵CD是⊙O的切線， ∴∠OCD＝90°， 即∠BCD＋∠OCB＝90°. ∵四邊形OABC是平行四邊形，∴OC∥AD. ∴∠OCB＝∠CBD. ∴∠BCD＋∠CBD＝90°. ∴∠ADC＝180°－9

9、0°＝90°. (2)連接OB. 由圓的性質(zhì)，知OA＝OB＝OC. ∵四邊形OABC是平行四邊形， ∴OC＝AB.∴OA＝OB＝AB. ∴△OAB是等邊三角形.∴∠AOB＝60°. ∵OF∥CD，∠ADC＝90°，∴OF⊥AB. ∴OF平分∠AOB. ∴∠FAB＝∠BOF＝∠AOB＝15°. 18.(14分)如圖，四邊形ABCD內(nèi)接于⊙O，對(duì)角線AC為⊙O的直徑，過(guò)點(diǎn)C作AC的垂線交AD的延長(zhǎng)線于點(diǎn)E，點(diǎn)F為CE的中點(diǎn)，連接DB，DC，DF. (1)求∠CDE的度數(shù)； (2)求證：DF是⊙O的切線； (3)若AC＝2 DE，求tan∠ABD的值. 解：(1

10、)∵AC為⊙O的直徑， ∴∠ADC＝90°. ∴∠CDE＝90°. (2)證明：連接OD. ∵∠CDE＝90°，點(diǎn)F為CE中點(diǎn)， ∴DF＝CE＝CF.∴∠FDC＝∠FCD. 又∵OD＝OC，∴∠ODC＝∠OCD. ∴∠ODC＋∠FDC＝∠OCD＋∠FCD. ∴∠ODF＝∠OCF. ∵EC⊥AC，∴∠OCF＝90°. ∴∠ODF＝90°. 又∵OD是⊙O的半徑， ∴DF為⊙O的切線. (3)在△ACD與△ACE中，∠ADC＝∠ACE＝90°，∠EAC＝∠CAD， ∴△ACD∽△AEC. ∴＝，即AC 2＝AD·AE. 又∵AC＝2 DE， ∴20DE2＝(AE－DE)·AE. ∴(AE－5DE)(AE＋4DE)＝0. ∴AE＝5DE.∴AD＝4DE. ∵在Rt△ACD中，AC2＝AD2＋CD2， ∴CD＝2DE. 又在⊙O中，∠ABD＝∠ACD， ∴tan∠ABD＝tan∠ACD＝＝2. 7