（安徽專版）2018年秋九年級數(shù)學(xué)下冊 周測（24.1）習(xí)題 （新版）滬科版

《（安徽專版）2018年秋九年級數(shù)學(xué)下冊 周測（24.1）習(xí)題 （新版）滬科版》由會員分享，可在線閱讀，更多相關(guān)《（安徽專版）2018年秋九年級數(shù)學(xué)下冊 周測（24.1）習(xí)題 （新版）滬科版（6頁珍藏版）》請在裝配圖網(wǎng)上搜索。

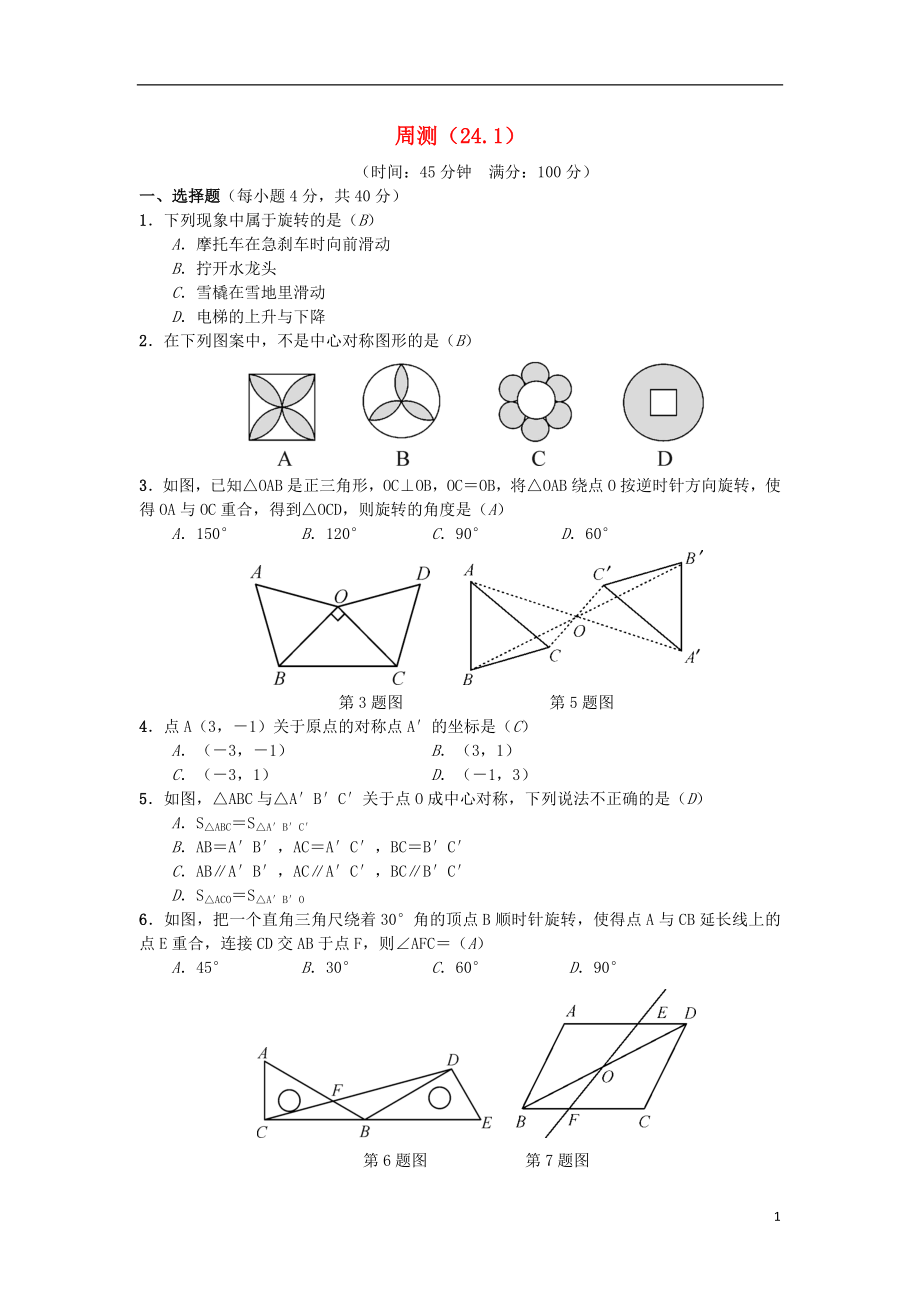
1、 周測（24.1） （時間：45分鐘　滿分：100分）　　　　　　　　　　　　　　　　 一、選擇題（每小題4分，共40分） 1．下列現(xiàn)象中屬于旋轉(zhuǎn)的是（B） A．摩托車在急剎車時向前滑動 B．?dāng)Q開水龍頭 C．雪橇在雪地里滑動 D．電梯的上升與下降 2．在下列圖案中，不是中心對稱圖形的是（B） 3．如圖，已知△OAB是正三角形，OC⊥OB，OC＝OB，將△OAB繞點O按逆時針方向旋轉(zhuǎn)，使得OA與OC重合，得到△OCD，則旋轉(zhuǎn)的角度是（A） A．150° B．120° C．90° D．60° 第3題圖 　　第5題圖

2、 4．點A（3，－1）關(guān)于原點的對稱點A′的坐標(biāo)是（C） A．（－3，－1） B．（3，1） C．（－3，1） D．（－1，3） 5．如圖，△ABC與△A′B′C′關(guān)于點O成中心對稱，下列說法不正確的是（D） A．S△ABC＝S△A′B′C′ B．AB＝A′B′，AC＝A′C′，BC＝B′C′ C．AB∥A′B′，AC∥A′C′，BC∥B′C′ D．S△ACO＝S△A′B′O 6．如圖，把一個直角三角尺繞著30°角的頂點B順時針旋轉(zhuǎn)，使得點A與CB延長線上的點E重合，連接CD交AB于點F，則∠AFC＝（A） A．45° B．30° C．60

3、° D．90° 第6題圖 　　第7題圖 7．如圖，點O是?ABCD的對稱中心，EF是過點O的任意一條直線，它將平行四邊形分成兩部分，四邊形ABFE和四邊形EFCD的面積分別記為S1，S2，那么S1，S2之間的關(guān)系為（C） A．S1>S2 B．S1

4、題圖 9．如圖，在方格紙上△DEF是由△ABC繞定點P順時針旋轉(zhuǎn)得到的．如果用（2，1）表示方格紙上A點的位置，（1，2）表示B點的位置，那么點P的位置為（A） A．（5，2） B．（2，5） C．（2，1） D．（1，2） 10．如圖，已知菱形OABC的頂點O（0，0），B（2，2）．若菱形繞點O逆時針旋轉(zhuǎn)，每秒旋轉(zhuǎn)45°，則第60秒時，菱形的對角線交點D的坐標(biāo)為（B） A．（1，－1） B．（－1，－1） C．（，0） D．（0，－） 二、填空題（每小題4分，共16分） 11．等邊三角形至少旋轉(zhuǎn)120度才能與自身重合． 12．如圖，Rt△ABC

5、的斜邊AB＝16，Rt△ABC繞點O順時針旋轉(zhuǎn)后得到Rt△A′B′C′，則Rt△A′B′C′的斜邊A′B′上的中線C′D的長度為8． 第12題圖 　　第13題圖 13．如圖，在△ABC中，∠ACB＝90°，AC＝4，BC＝3.將△ABC繞點A逆時針旋轉(zhuǎn)，使點C落在線段AB上的點E處，點B落在點D處，連接CE，則△CBE的面積為． 14．如圖，在矩形ABCD中，AB＝2，BC＝1，將矩形ABCD繞點A順時針旋轉(zhuǎn)90°得矩形AEFG，連接CG，EG，則∠CGE＝45°． 三、解答題（共44分） 15．（6分）平面直角坐標(biāo)系第二象限內(nèi)的點P（x2＋2x，3）與另一點

6、Q（x＋2，y）關(guān)于原點對稱，試求x＋2y的值． 解：根據(jù)題意，得（x2＋2x）＋（x＋2）＝0，y＝－3. 解得x1＝－1，x2＝－2. ∵點P在第二象限，∴x2＋2x<0.∴x＝－1. ∴x＋2y＝－7. 16．（8分）如圖，正方形網(wǎng)格中的每個小正方形邊長都是1，請按要求分別在圖1和圖2中畫出相應(yīng)的圖形，所畫的圖形的各個頂點均在格點上（每個小正方形的頂點均為格點）． （1）請在圖1中畫一個面積為7.5的△ABE； （2）請在圖2中畫一個四邊形ABCD，使得它是一個中心對稱圖形，且相鄰兩邊之比為2∶1，并直接寫出AC的長． 解：（1）如圖1所示，△ABC即為所求（

7、答案不唯一）． （2）如圖2所示，四邊形ABCD即為所求，AC＝. 17．（8分）如圖，方格紙中每個小正方形的邊長都是1個單位長度，Rt△ABC的三個頂點A（－2，2），B（0，5），C（0，2）． （1）將△ABC以點C為旋轉(zhuǎn)中心旋轉(zhuǎn)180°，得到△A1B1C，請畫出△A1B1C的圖形； （2）平移△ABC，使點A的對應(yīng)點A2的坐標(biāo)為（－2，－6），請畫出平移后對應(yīng)的△A2B2C2的圖形； （3）若將△A1B1C繞某一點旋轉(zhuǎn)可得到△A2B2C2，請直接寫出旋轉(zhuǎn)中心的坐標(biāo)． 解：（1）（2）如圖． （3）旋轉(zhuǎn)中心的坐標(biāo)為（0，－2）． 18．（10分）如圖，四邊形A

8、BCD是正方形，E，F(xiàn)分別是DC和CB的延長線上的點，且DE＝BF，連接AE，AF，EF. （1）求證：△ADE≌△ABF； （2）若BC＝8，DE＝6，求△AEF的面積． 解：（1）證明：∵四邊形ABCD是正方形， ∴AD＝AB，∠D＝∠ABC＝90°. ∵F是CB的延長線上的點， ∴∠ABF＝90°. 在△ADE和△ABF中， ∴△ADE≌△ABF（SAS）． （2）∵BC＝8，∴AD＝8. 在Rt△ADE中，AE＝＝10. ∵△ABF可以由△ADE繞旋轉(zhuǎn)中心A點順時針旋轉(zhuǎn)90度得到，∴AE＝AF，∠EAF＝90°. ∴S△AEF＝AE2＝×100＝50.

9、 19．（12分）如圖1放置的一副三角尺，將含45°角的三角尺以斜邊中點O為旋轉(zhuǎn)中心，逆時針旋轉(zhuǎn)30°，如圖2，連接OB，OD，AD. （1）求證：△AOB≌△AOD； （2）試判定四邊形ABOD是什么四邊形，并說明理由． 解：（1）證明：根據(jù)題意，得∠BAC＝60°，∠ABC＝∠EDF＝90°，EF＝AC，OD⊥EF， ∵O為AC，EF的中點， ∴OB＝AC，OD＝EF. 又∵AC＝EF， ∴OB＝OD＝OA. ∵∠BAO＝60°， ∴△AOB是等邊三角形． ∴∠AOB＝60°，AB＝OB＝OA. ∵△DEF繞斜邊中點O逆時針旋轉(zhuǎn)30°得到圖2， ∴∠AOE＝30°. ∴∠AOD＝90°－30°＝60°. ∴△AOD為等邊三角形． ∴△AOB≌△AOD. （2）四邊形ABOD是菱形． 理由如下：∵△AOB≌△AOD， ∴AB＝AD. ∴AB＝AD＝OB＝OD. ∴四邊形ABOD是菱形． 6