（安徽專用）2013年高考數(shù)學總復習 第七章第1課時 空間幾何體的結(jié)構(gòu)及其三視圖和直觀圖課時闖關（含解析）

《（安徽專用）2013年高考數(shù)學總復習 第七章第1課時 空間幾何體的結(jié)構(gòu)及其三視圖和直觀圖課時闖關（含解析）》由會員分享，可在線閱讀，更多相關《（安徽專用）2013年高考數(shù)學總復習 第七章第1課時 空間幾何體的結(jié)構(gòu)及其三視圖和直觀圖課時闖關（含解析）（4頁珍藏版）》請在裝配圖網(wǎng)上搜索。

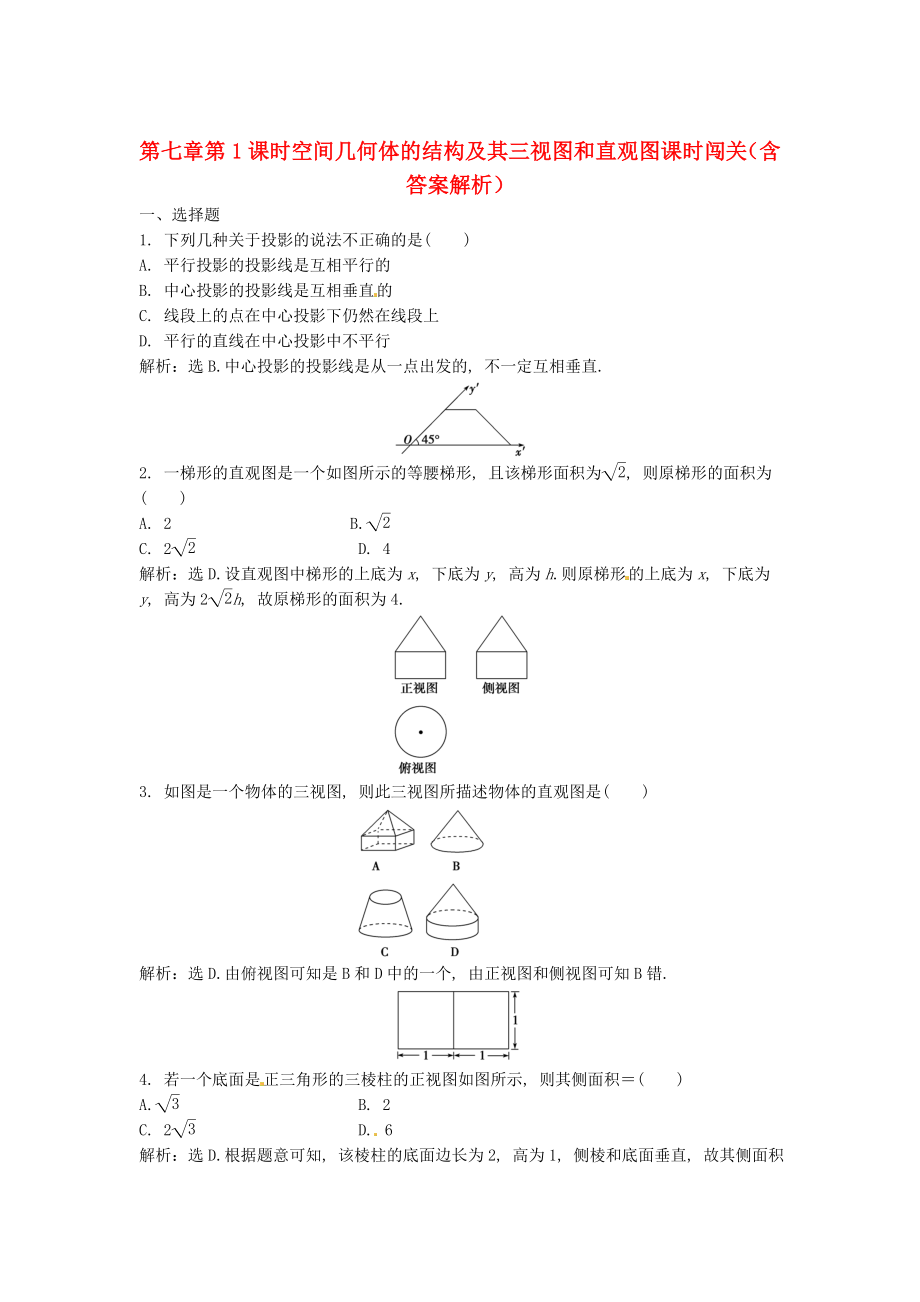
1、第七章第1課時 空間幾何體的結(jié)構(gòu)及其三視圖和直觀圖 課時闖關（含答案解析）一、選擇題1. 下列幾種關于投影的說法不正確的是()A. 平行投影的投影線是互相平行的B. 中心投影的投影線是互相垂直的C. 線段上的點在中心投影下仍然在線段上D. 平行的直線在中心投影中不平行解析：選B.中心投影的投影線是從一點出發(fā)的, 不一定互相垂直. 2. 一梯形的直觀圖是一個如圖所示的等腰梯形, 且該梯形面積為, 則原梯形的面積為()A. 2B.C. 2 D. 4解析：選D.設直觀圖中梯形的上底為x, 下底為y, 高為h.則原梯形的上底為x, 下底為y, 高為2h, 故原梯形的面積為4.3. 如圖是一個物體的三視

2、圖, 則此三視圖所描述物體的直觀圖是()解析：選D.由俯視圖可知是B和D中的一個, 由正視圖和側(cè)視圖可知B錯. 4. 若一個底面是正三角形的三棱柱的正視圖如圖所示, 則其側(cè)面積()A. B. 2C. 2 D. 6解析：選D.根據(jù)題意可知, 該棱柱的底面邊長為2, 高為1, 側(cè)棱和底面垂直, 故其側(cè)面積為2136.5. 如圖是長和寬分別相等的兩個矩形, 給定下列三個命題：存在三棱柱, 其正視圖、俯視圖如右圖; 存在四棱柱, 其正視圖、俯視圖如右圖; 存在圓柱, 其正視圖、俯視圖如右圖. 其中真命題的個數(shù)是()A. 3 B. 2C. 1 D. 0解析：選A.底面是等腰直角三角形的三棱柱, 當它的一

3、個矩形側(cè)面放置在水平面上時, 它的正視圖和俯視圖可以是全等的矩形, 因此正確; 若長方體的高和寬相等, 則存在滿足題意的兩個相等的矩形, 因此正確; 當圓柱側(cè)放時(即側(cè)視圖為圓時), 它的正視圖和俯視圖可以是全等的矩形, 因此正確. 二、填空題6. 如圖, 在正方體ABCDA1B1C1D1中, 點P是上底面A1B1C1D1內(nèi)一動點, 則三棱錐PABC的正視圖與側(cè)視圖的面積的比值為_. 解析：依題意得三棱錐PABC的正視圖與側(cè)視圖分別是一個三角形, 且這兩個三角形的底邊長都等于正方體的棱長, 底邊上的高也都相等, 因此三棱錐PABC的正視圖與側(cè)視圖的面積之比等于1.答案：17. (2012開封調(diào)

4、研)給出下列命題：在圓柱的上、下底面的圓周上各取一點, 則這兩點的連線是圓柱的母線; 圓錐的頂點與底面圓周上任意一點的連線是圓錐的母線; 在圓臺的上、下底面的圓周上各取一點, 則這兩點的連線是圓臺的母線; 圓柱的任意兩條母線所在的直線是互相平行的. 其中正確命題的序號是_. 解析：根據(jù)圓柱、圓錐、圓臺的定義和性質(zhì)可知, 只有兩個命題是正確的. 答案：8. 若正三棱錐(底面為正三角形, 頂點與底面中心的連線垂直于底面)的正視圖與俯視圖如圖所示(單位：cm), 則它的側(cè)視圖的面積為_cm2.解析：由該正三棱錐的正視圖和俯視圖可知, 其側(cè)視圖為一個三角形, 它的底邊長等于俯視圖的高即, 高等于正視圖

5、的高即, 所以側(cè)視圖的面積為S(cm2). 答案：三、解答題9. 圓臺的一個底面周長是另一個底面周長的3倍, 軸截面的面積等于392, 母線與軸的夾角為45, 求這個圓臺的高、母線長和底面半徑. 解：作出圓臺的軸截面如圖. 設OAr, 一底面周長是另一底面周長的3倍, OA3r, SAr, SA3r, OO2r.由軸截面的面積為(2r6r)2r392, 得r7.故上底面半徑為7, 下底面半徑為21, 高為14, 母線長為14.10. 根據(jù)圖中幾何體的三視圖畫出對應的幾何體. 解：它們的直觀圖分別是圖中的(1)、(2)、(3). 11. 如圖, 在四棱錐PABCD中, 底面為正方形, PC與底面ABCD垂直, 圖為該四棱錐的正視圖和側(cè)視圖, 它們是腰長為6 cm的全等的等腰直角三角形. (1)根據(jù)圖所給的正視圖、側(cè)視圖, 畫出相應的俯視圖, 并求出該俯視圖的面積; (2)求PA.解：(1)該四棱錐的俯視圖為(內(nèi)含對角線), 邊長為6 cm的正方形, 如圖, 其面積為36 cm2.(2)由側(cè)視圖可求得PD6.由正視圖可知AD6, 且ADPD, 所以在RtAPD中, PA6 cm.