《高中數(shù)學(xué) 第一章4 空間圖形的基本關(guān)系與公理第2課時(shí)目標(biāo)導(dǎo)學(xué) 北師大版必修2》由會(huì)員分享�����,可在線閱讀,更多相關(guān)《高中數(shù)學(xué) 第一章4 空間圖形的基本關(guān)系與公理第2課時(shí)目標(biāo)導(dǎo)學(xué) 北師大版必修2(5頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索����。
1、
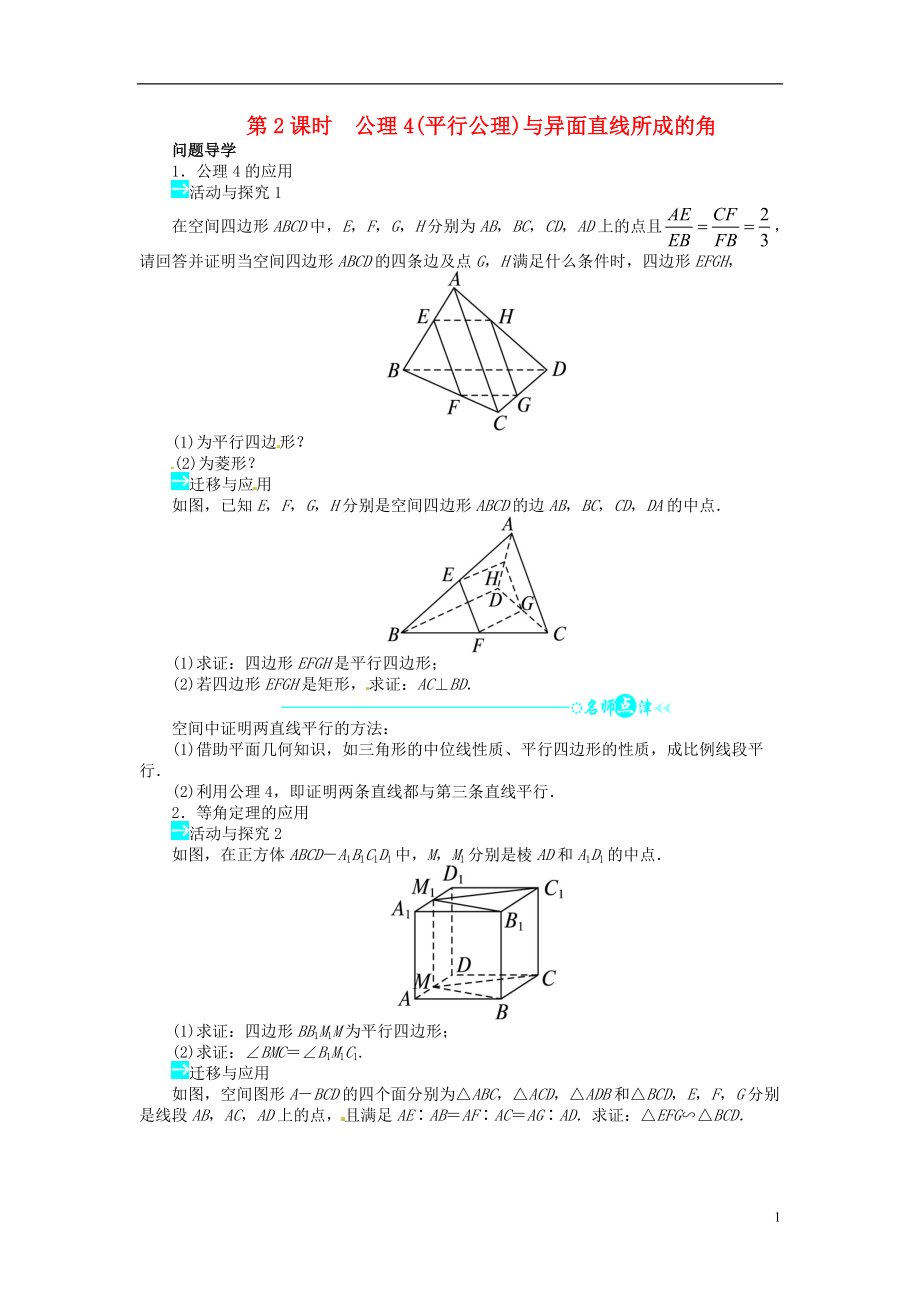
第2課時(shí) 公理4(平行公理)與異面直線所成的角
問題導(dǎo)學(xué)
1.公理4的應(yīng)用
活動(dòng)與探究1
在空間四邊形ABCD中�����,E����,F(xiàn),G���,H分別為AB��,BC�����,CD�����,AD上的點(diǎn)且�����,請(qǐng)回答并證明當(dāng)空間四邊形ABCD的四條邊及點(diǎn)G�,H滿足什么條件時(shí),四邊形EFGH����,
(1)為平行四邊形?
(2)為菱形��?
遷移與應(yīng)用
如圖��,已知E�,F(xiàn),G����,H分別是空間四邊形ABCD的邊AB,BC�����,CD����,DA的中點(diǎn).
(1)求證:四邊形EFGH是平行四邊形;
(2)若四邊形EFGH是矩形�,求證:AC⊥BD.
空間中證明兩直線平行的方法:
(1)借助平面幾何知識(shí),如三角形的中位線性質(zhì)�、平行四邊
2、形的性質(zhì)���,成比例線段平行.
(2)利用公理4�����,即證明兩條直線都與第三條直線平行.
2.等角定理的應(yīng)用
活動(dòng)與探究2
如圖����,在正方體ABCD-A1B1C1D1中��,M��,M1分別是棱AD和A1D1的中點(diǎn).
(1)求證:四邊形BB1M1M為平行四邊形�;
(2)求證:∠BMC=∠B1M1C1.
遷移與應(yīng)用
如圖,空間圖形A-BCD的四個(gè)面分別為△ABC����,△ACD,△ADB和△BCD,E���,F(xiàn)�,G分別是線段AB���,AC��,AD上的點(diǎn)�����,且滿足AE∶AB=AF∶AC=AG∶AD.求證:△EFG∽△BCD.
1.要明確等角定理的兩個(gè)條件����,即兩個(gè)角的兩條邊分別對(duì)應(yīng)平行���,并且方向相同���,這兩個(gè)
3、條件缺一不可.
2.空間中證明兩個(gè)角相等��,可以利用等角定理�����,也可以利用三角形的相似或全等,還可以利用平行四邊形的對(duì)角相等.在利用等角定理時(shí)�����,關(guān)鍵是弄清楚兩個(gè)角對(duì)應(yīng)邊的關(guān)系.
3.異面直線及其所成的角
活動(dòng)與探究3
如圖����,已知正方體ABCD-A′B′C′D′.
(1)哪些棱所在的直線與直線BC′是異面直線�?
(2)求異面直線AD′與B′C、A′C與AB所成角的正切值.
遷移與應(yīng)用
已知正方體ABCD-A′B′C′D′����,求:
(1)BC′與CD′所成的角;
(2)AD與BC′所成的角.
由異面直線所成角的定義求異面直線所成角的一般步驟是:平移→構(gòu)造三角形→解三角形
4����、→作答.在幾何體中進(jìn)行平移構(gòu)造異面直線所成角時(shí),一般選擇兩異面直線中一條上的一點(diǎn)���,或幾何體頂點(diǎn)�、棱的中點(diǎn)等特殊點(diǎn).
當(dāng)堂檢測(cè)
1.空間兩個(gè)角α�,β的兩邊分別對(duì)應(yīng)平行,且α=50,則β等于( ).
A.50 B.130 C.40 D.50或130
2.空間四邊形的兩條對(duì)角線長(zhǎng)度相等����,順次連接四條邊的中點(diǎn)得到的四邊形是( ).
A.梯形 B.平行四邊形
C.菱形 D.矩形
3.如圖,正方體ABCD-A1B1C1D1中��,E��,F(xiàn)分別是棱BC���,CC1的中點(diǎn)��,則異面直線EF與B1D1所成的角為________.
(第3題圖)
4.
5����、如圖所示���,在三棱錐P-ABC的六條棱所在的直線中����,異面直線共有________對(duì).
(第4題圖)
提示:用最精練的語言把你當(dāng)堂掌握的核心知識(shí)的精華部分和基本技能的要領(lǐng)部分寫下來并進(jìn)行識(shí)記.
答案:
課前預(yù)習(xí)導(dǎo)學(xué)
預(yù)習(xí)導(dǎo)引
1.平行 a∥c
預(yù)習(xí)交流1 提示:(1)本質(zhì):表明了空間中線線平行的傳遞性.
(2)作用:公理4給出了空間兩條直線平行的一種證明方法.它是論證平行問題的主要依據(jù)之一�,也是研究空間兩直線的位置關(guān)系、直線與平面位置關(guān)系的基礎(chǔ).
(3)關(guān)鍵:尋找第三條直線分別與前兩條直線平行是應(yīng)用公理4證明線線平行的關(guān)鍵.
2.相等或互補(bǔ)
預(yù)習(xí)交流2
6��、 提示:相等;互補(bǔ).
3.不在
預(yù)習(xí)交流3 提示:一定不相交.若對(duì)角線相交��,則四個(gè)頂點(diǎn)共面�,這與定義中四個(gè)頂點(diǎn)不共面相矛盾.
4.銳角 直角 互相垂直
預(yù)習(xí)交流4 提示:兩條異面直線所成角的范圍是(0,90].
課堂合作探究
問題導(dǎo)學(xué)
活動(dòng)與探究1 思路分析:由==����,可想到證明EF∥AC;為使四邊形EFGH為平行四邊形�����,需證明GH=EF�����,且GH∥AC�;為使四邊形EFGH為菱形����,在(1)成立的情況下,還需證明EH=EF��,進(jìn)一步可得AC���,BD的關(guān)系.
解:(1)當(dāng)==時(shí)��,
四邊形EFGH為平行四邊形.
理由:∵==�����,
∴EF∥AC且EF=AC.
若==����,
則HG∥AC且H
7、G=AC.
∴EF∥HG����,EF=HG,
∴四邊形EFGH為平行四邊形.
(2)當(dāng)==且AC=BD時(shí)���,四邊形EFGH為菱形.
理由:由(1)知����,若==����,
則四邊形EFGH為平行四邊形,且EF=AC��,EH=BD.若AC=BD,則EF=AC=BD=EH.
∴平行四邊形EFGH為菱形.
遷移與應(yīng)用 證明:(1)如題圖�,在△ABD中,
∵EH是△ABD的中位線����,
∴EH∥BD,EH=BD.
又FG是△CBD的中位線�,
∴FG∥BD,F(xiàn)G=BD�����,
∴FG∥EH���,∴E,F(xiàn)���,G�����,H四點(diǎn)共面.又FG=EH���,
∴四邊形EFGH是平行四邊形.
(2)由(1)知EH∥BD����,同理AC∥GH.
8�����、
∵四邊形EFGH是矩形���,
∴EH⊥GH.∴AC⊥BD.
活動(dòng)與探究2 思路分析:(1)欲證四邊形BB1M1M是平行四邊形�,可證其一組對(duì)邊平行且相等��;(2)可結(jié)合(1)利用定理證明或利用三角形全等證明.
證明:(1)在正方形ADD1A1中�,M,M1分別為AD����,A1D1的中點(diǎn),
∴MM1=AA1�,MM1∥AA1.
又∵AA1=BB1,AA1∥BB1����,
∴MM1∥BB1,且MM1=BB1�����,
∴四邊形BB1M1M為平行四邊形.
(2)方法一:由(1)知四邊形BB1M1M為平行四邊形,
∴B1M1∥BM.
同理可得四邊形CC1M1M為平行四邊形���,
∴C1M1∥CM.
由平面幾
9��、何知識(shí)可知����,∠BMC和∠B1M1C1都是銳角���,
∴∠BMC=∠B1M1C1.
方法二:由(1)知四邊形BB1M1M為平行四邊形����,
∴B1M1=BM.
同理可得四邊形CC1M1M為平行四邊形.
∴C1M1=CM.
又∵B1C1=BC���,∴△BCM≌△B1C1M1.
∴∠BMC=∠B1M1C1.
遷移與應(yīng)用 證明:在△ABD中,
∵AE∶AB=AG∶AD�����,
∴EG∥BD.同理�,GF∥DC����,EF∥BC.
又∠GEF與∠DBC兩組對(duì)邊方向分別相同���,∴∠GEF=∠DBC.
同理�����,∠EGF=∠BDC.
∴△EFG∽△BCD.
活動(dòng)與探究3 思路分析:(1)按照異面直線的定義進(jìn)行判
10�、斷��;(2)根據(jù)異面直線所成角的定義進(jìn)行求解.
解:(1)所在直線與BC′是異面直線的棱有:AA′�,DD′,A′B′�����,DC��,AD��,A′D′.
(2)因?yàn)锳D′∥BC′��,所以AD′與B′C所成的角就是BC′與B′C所成的角,而BC′⊥B′C�����,所以AD′與B′C所成的角等于90���,其正切值不存在.
因?yàn)锳B∥CD���,所以∠A′CD就是異面直線A′C與AB所成的角.
在△A′CD中,若設(shè)正方體棱長(zhǎng)為a�����,則CD=a����,A′D=a,A′C=a����,
因此△A′CD是直角三角形,
于是tan∠A′CD==.
遷移與應(yīng)用 解:(1)連接BA′��,則BA′∥CD′�����,
則∠A′BC′就是BC′與CD′所成的角.
連接A′C′��,由△A′BC′為正三角形�����,知∠A′BC′=60.
即BC′與CD′所成的角為60.
(2)由AD∥BC����,知AD與BC′所成的角就是∠C′BC.易知∠C′BC=45.
當(dāng)堂檢測(cè)
1.D 2.C 3.60 4.3
5
 高中數(shù)學(xué) 第一章4 空間圖形的基本關(guān)系與公理第2課時(shí)目標(biāo)導(dǎo)學(xué) 北師大版必修2
高中數(shù)學(xué) 第一章4 空間圖形的基本關(guān)系與公理第2課時(shí)目標(biāo)導(dǎo)學(xué) 北師大版必修2