《精校版高一數(shù)學(xué)人教B版必修4雙基限時(shí)練20 平面向量基本定理 Word版含解析》由會員分享����,可在線閱讀,更多相關(guān)《精校版高一數(shù)學(xué)人教B版必修4雙基限時(shí)練20 平面向量基本定理 Word版含解析(11頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索�。
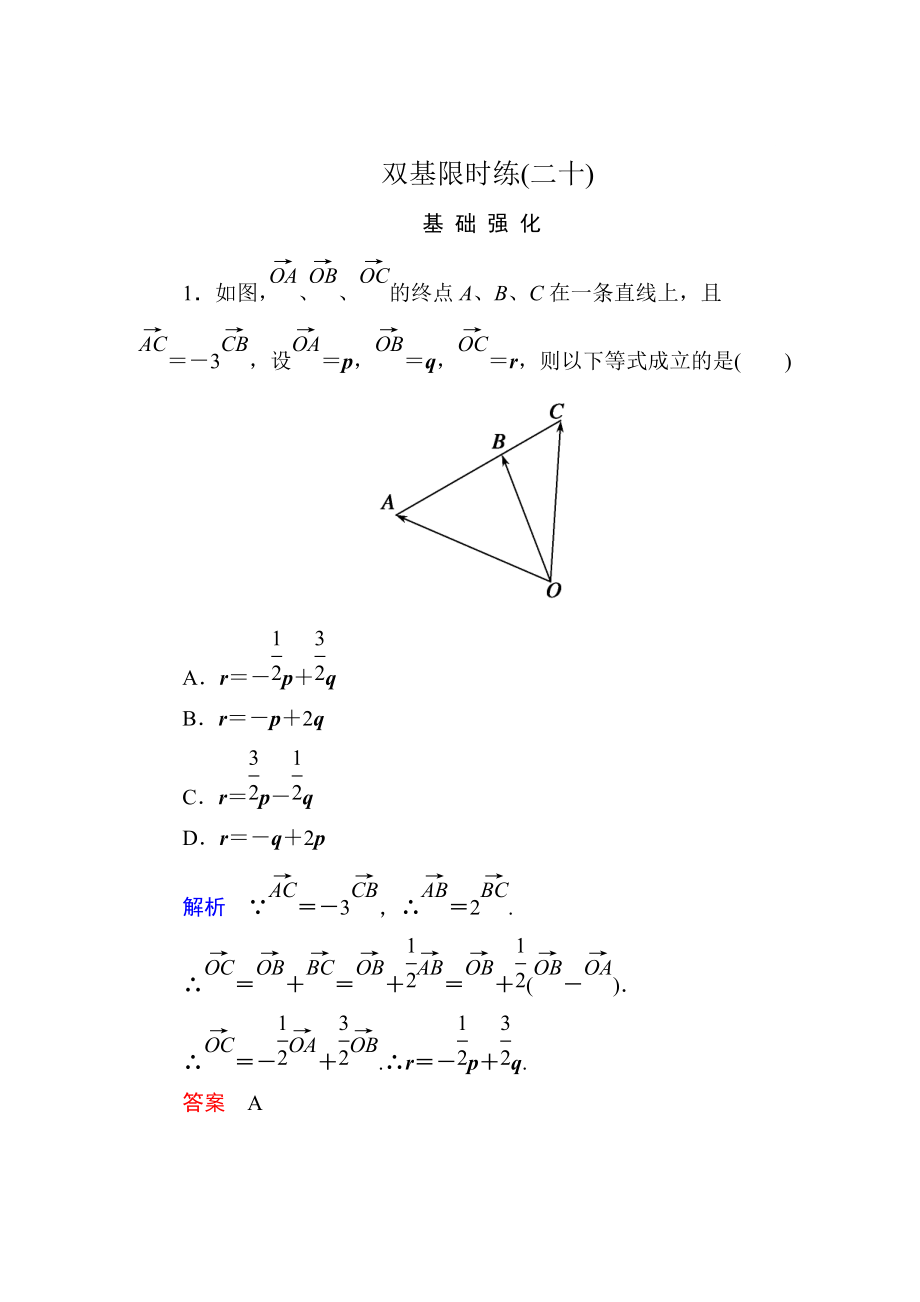
1、最新資料最新資料最新資料最新資料最新資料雙基限時(shí)練(二十)基 礎(chǔ) 強(qiáng) 化1如圖�����,�、的終點(diǎn)A、B��、C在一條直線上����,且3,設(shè)p���,q����,r,則以下等式成立的是()ArpqBrp2qCrpqDrq2p解析3�����,2.().rpq.答案A2已知平面內(nèi)不共線的四點(diǎn)O���,A�,B��,C��,滿足��,則|:|()A1:|3B3:|1C1:|2D2:|1解析��,()()����,2.|2|.|:|2:|1.答案D3非零不共線向量�、,且2xy���,若(R)����,則點(diǎn)Q(x,y)的軌跡方程是()Axy20 B2xy10Cx2y20 D2xy20解析����,()(1).2(22)2,x�����,y滿足xy20.點(diǎn)Q(x��,y)的軌跡方程為xy20.答案A4ABC中����,點(diǎn)
2、D在邊AB上��,CD平分ACB��,a���,b����,|a|1,|b|2�����,則()A.ab B.abC.ab D.ab解析CD是ACB的角平分線��,2.()ab.答案B5若點(diǎn)M是ABC的重心��,則下列各向量中與共線的是()A. B.C. D3解析如圖��,設(shè)D��,E����,F(xiàn)分別為各邊的中點(diǎn)��,()同理()���,()0�����,0與共線答案C6如圖在ABC中�����,AHBC于H��,M為AH的中點(diǎn)�����,若�����,則的值為()A1 B.C1 D2解析B��、H���、C三點(diǎn)共線�,(1t)t.2(1t)t.���,.答案B7如圖��,在平行四邊形ABCD中����,點(diǎn)O為AC的中點(diǎn),點(diǎn)N為OB的中點(diǎn)����,設(shè)a,b���,若用a���,b來表示向量, 則_.解析以a��,b作為以A點(diǎn)為公共起點(diǎn)的一組基底���,則()a
3��、b.答案ab8向量a在基底e1�����,e2下可以表示為a2e13e2,be1e2��,ce1e2,若a在基底b�,c下可表示為abc,則_���,_. 答案����,能 力 提 升9如圖�����,平面內(nèi)三個(gè)向量���,其中AOB120°�����,AOC30°�����,且|1��,|2����,若(,R)��,則的值為_解析以O(shè)A���、OB為鄰邊作平行四邊形OECF�,如圖所示則.即���,.AOB120°���,AOC30°,BOC90°.在COF中�,|2,OCF30°�����,|2�,|4,|4.|1.4�����,2.42.4����,2,6.答案610已知四邊形ABCD為矩形�,且AD2AB,又ADE為等腰直角三角形�,F(xiàn)為ED的中點(diǎn),e1���,e2����,
4���、選擇e1����,e2作為基底���,用基底表示向量�����,.解析如圖���,e1�����,e2��,e2e1.由已知AD2ABDE��,且F為DE的中點(diǎn)�����,四邊形ABDF為平行四邊形e2���,22e2e1.e2e1.11設(shè)e1,e2是不共線的非零向量�����,且ae12e2��,be13e2.(1)證明:a,b可以作為一組基底��;(2)以a���,b為基底,求向量c3e1e2的分解式���;(3)若4e13e2ab�,求�����,的值解析(1)若a��,b共線����,則存在R,使ab����,則e12e2(e13e2)由e1,e2不共線��,得不存在,故a與b不共線��,可以作為一組基底(2)設(shè)cmanb(m����,nR),得3e1e2m(e12e2)n(e13e2)(mn)e1(2m3n)e2.c2ab
5�����、.(3)由4e13e2ab�����,得4e13e2(e12e2)(e13e2)()e1(23)e2.故所求���,的值分別為3和1.12平面內(nèi)有一個(gè)ABC和一點(diǎn)O(如圖)����,線段OA���、OB��、OC的中點(diǎn)分別為E��、F�、G,BC��、CA��、AB的中點(diǎn)分別為L�、M、N���,設(shè)a,b���,c.(1)試用a�、b�、c表示向量、�����;(2)證明:線段EL����、FM���、GN交于一點(diǎn)且互相平分解析(1)a,(bc)��,(bca)同理:(acb)���,(abc)(2)證明:設(shè)線段EL的中點(diǎn)為P1��,則()(abc)設(shè)FM���、GN的中點(diǎn)分別為P2、P3�,同理可求得(abc),(abc).即EL�、FM、GN交于一點(diǎn)�����,且互相平分品 味 高 考13設(shè)a是已知的平面向量且a0��,關(guān)于向量a的分解����,有如下四個(gè)命題:給定向量b�,總存在向量c�,使abc;給定向量b和c�����,總存在實(shí)數(shù)和��,使abc�;給定單位向量b和正數(shù),總存在單位向量c和實(shí)數(shù)�,使abc;給定正數(shù)和��,總存在單位向量b和單位向量c����,使abc����;上述命題中的向量b,c和a在同一平面內(nèi)且兩兩不共線�����,則正確命題的個(gè)數(shù)是()A1 B2C3 D4解析利用向量加法的三角法則,易得對��;利用平面向量的基本定理�����,易得對�����;以a的終點(diǎn)作長度為的圓���,這個(gè)圓必須和向量b有交點(diǎn)���,這個(gè)不一定能滿足,故錯(cuò)�����;利用向量加法的三角形法則���,結(jié)合三角形兩邊之和大于第三邊����,即必須|b|c|a|,故錯(cuò)答案B最新精品資料
 精校版高一數(shù)學(xué)人教B版必修4雙基限時(shí)練20 平面向量基本定理 Word版含解析
精校版高一數(shù)學(xué)人教B版必修4雙基限時(shí)練20 平面向量基本定理 Word版含解析