《2018年高中數(shù)學 第二章 解析幾何初步 2.1.3 兩條直線的位置關系課件 北師大版必修2.ppt》由會員分享�����,可在線閱讀�,更多相關《2018年高中數(shù)學 第二章 解析幾何初步 2.1.3 兩條直線的位置關系課件 北師大版必修2.ppt(21頁珍藏版)》請在裝配圖網(wǎng)上搜索。
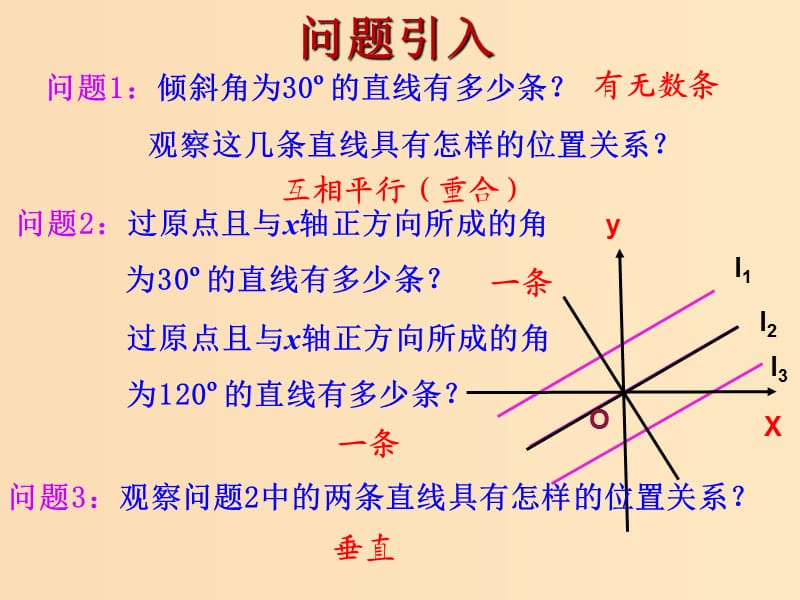
1����、問題2:過原點且與x軸正方向所成的角 為30的直線有多少條��?,問題1:傾斜角為30的直線有多少條�?,,有無數(shù)條,O,問題引入,觀察這幾條直線具有怎樣的位置關系?,一條,過原點且與x軸正方向所成的角為120的直線有多少條�����?,互相平行(重合),一條,問題3:觀察問題2中的兩條直線具有怎樣的位置關系?,垂直,,,,,,在平面直角坐標系中�,怎樣根據(jù)直線方程的特征(斜率)判斷兩條直線方程的位置關系呢?,平行,垂直,重合,,,思考:通過上面的實例總結出平面內兩直線的位置關 系有哪些��?,1.3 兩條直線的位置關系,我們可以知道����,斜率相等的兩條直線,探究點1 兩條直線平行,相等.,它們相互平行(重合)
2、�;,反之,兩條直線平行��,它們的,傾斜角,相等�,,若傾斜角不為90,,則它們的斜率,相等.,2,,傾斜角,斜率不存在時兩直線的平行,當兩條直線中有一條直線 沒有斜率時��,,那另一條直線 的斜率應該滿足什么條件��?���?,如果兩直線位置關系為:,互相平行,斜率不存在���,傾斜角為,90,l1,l2,斜率存在時兩直線的平行:,兩條直線 和 �����,,另一條直線的斜率為 0,如果����,兩直線位置關系為:,,互相垂直.,探究點2 兩條直線垂直,當兩條直線中有一條直線沒有斜率時��,,那另一條直線的斜率應該滿足什么條件�����?��?,已知直線 過原點作與 垂直的直線 �, 求 的斜率.,,,,,,思考1:兩條直線的斜率
3、存在時��,那怎樣用斜率來判斷兩條直線垂直?,解:設直線 的直線方程為:,那 的方向向量為:,的方向向量為:,解法一:,,,,,,,,為,,O,解法二:,思考2:當直線的斜率不存在時, l1l2k1k2=-1 還適用嗎?,當直線的斜率不存在時上述公式不適用���, 此時直線的傾斜角是90���,斜率不存在�����。,例1 判斷下列各對直線是否平行還是垂直����,并說明理由:,例題講解,解:設兩直線的斜率分別是 ��, �,在y軸上截距 分別是 , ,則 因為 所以 .,(2),(1),解:設兩直線的斜率分別是 則 有 所以,(3),解: 設兩直線的斜率分別是 則 有
4���、 所以,(4),(5),解:由方程可知, 軸�����, 軸,且兩直線在 軸上截距 不相等�,所以 .,思考3:能否根據(jù)直線方程的一般式來判斷兩 直線的位置關系呢�??,設,( 不全為0)���,,( 不全為0)����,,(1),與,平行,則,垂直,與,(2),例2 求過點 且平行于直線 的直線方程.,解:所求直線平行于直線 ,所以它們 的斜率相等�����,都為 而所求直線過 所以���,所求直線的方程為 ���, 即 .,解:已知直線 的斜率為 ,所求直線與已知直線垂直���,所以該直線的斜率為 ��, 且該直線過點 �, 因此所求直線方程為 �, 即,例3 求過點 且垂
5、直于直線 的直線方程.,1.已知不重合的兩條直線 �,下列說法中正確的是. 若直線 與 的斜率相等,則 ����; 若直線 �����,則兩直線的斜率相等�����; 若直線 的斜率不相等,則兩直線不平行�����; 若直線 的斜率均不存在�����,則 �; 如果直線 平行,且 的斜率不存在����,那么 的斜率也不存在.,,中斜率可能不存在,正確��。,2.直線x+ay-7=0與直線(a+1)x+2y-14=0互相平行�����,則a的值是( ) A.1 B.-2 C.1或-2 D.-1或2,B,3.若直線x+ay+1=0與直線(a+1)x-2y+3=0互相垂直,則實數(shù)a=_______.,1,4已知直
6�、線 l滿足下列條件,求直線l的方程. (1)經(jīng)過點A(3,2)且與直線4x+y-2=0平行; (2)經(jīng)過點B(3,0)且與直線2x+y-5=0垂直,解: (1)所求直線平行于直線 ��,所以它們的斜率相等�����,都為 而所求直線過 所求直線的方程為 ��,即 .,解:(2)已知直線 的斜率為 ��,所求直線 與已知直線垂直�,所以該直線的斜率為 ,且該直線過點 ���,因此所求直線方程為 ���, 即,斜率間的關系(若l1,l2的斜率都存在�,設l1:y=k1x+b1, l2:y=k2x+b2),l1l2k1=k2,且b1b2,l1l2 k1k2= -1,設,( 不全為0),,( 不全為0)�,,(1),與,平行,垂直,與,(2),直線方程的一般式來判斷兩直線的位置關系:,
 2018年高中數(shù)學 第二章 解析幾何初步 2.1.3 兩條直線的位置關系課件 北師大版必修2.ppt
2018年高中數(shù)學 第二章 解析幾何初步 2.1.3 兩條直線的位置關系課件 北師大版必修2.ppt