《(江蘇專用)高考數(shù)學(xué)總復(fù)習 考前三個月 考前回扣6 立體幾何 理-人教版高三數(shù)學(xué)試題》由會員分享��,可在線閱讀�����,更多相關(guān)《(江蘇專用)高考數(shù)學(xué)總復(fù)習 考前三個月 考前回扣6 立體幾何 理-人教版高三數(shù)學(xué)試題(6頁珍藏版)》請在裝配圖網(wǎng)上搜索����。
1�����、回扣6 立體幾何
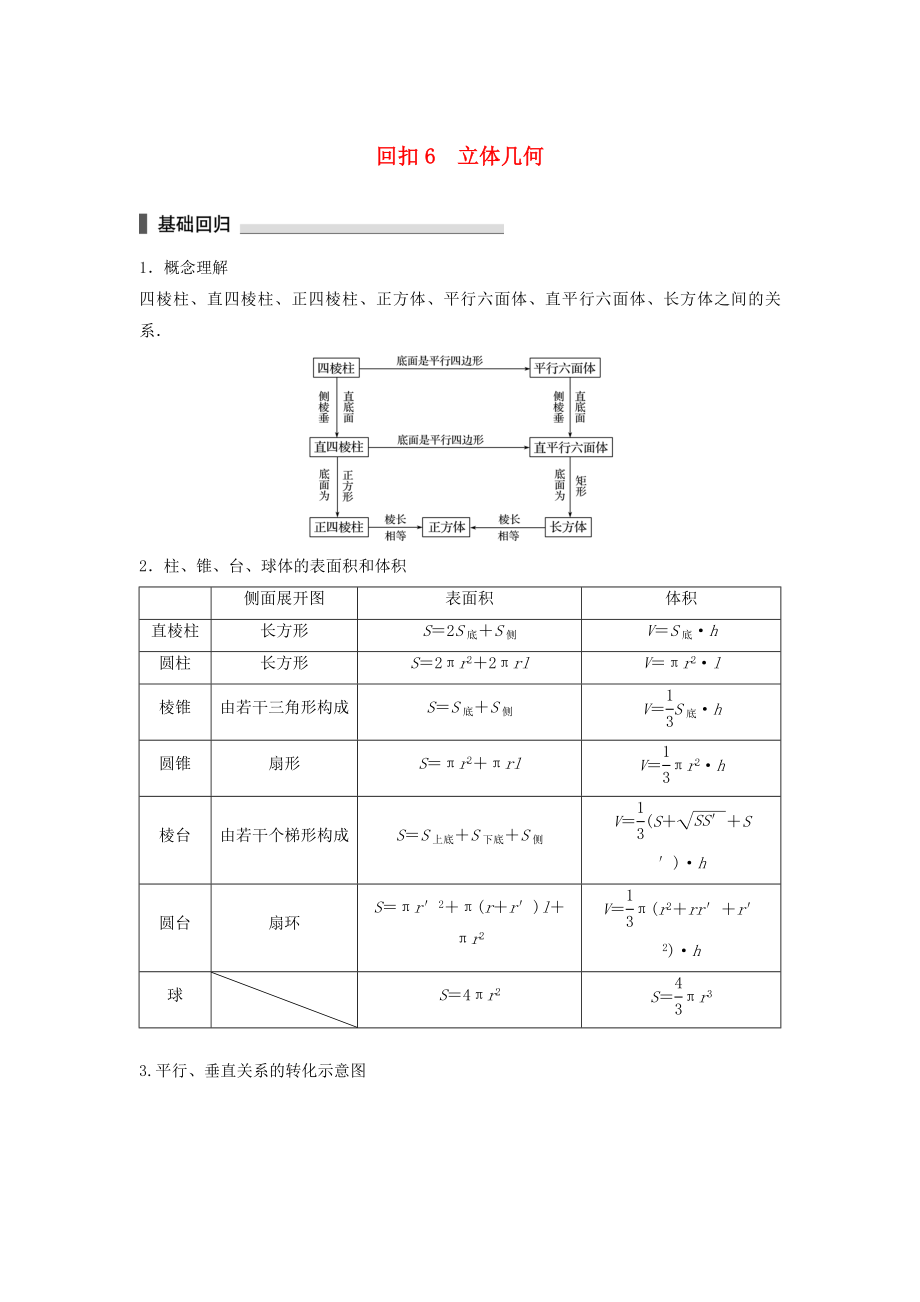
1.概念理解
四棱柱���、直四棱柱���、正四棱柱�、正方體�、平行六面體、直平行六面體��、長方體之間的關(guān)系.
2.柱�����、錐、臺�����、球體的表面積和體積
側(cè)面展開圖
表面積
體積
直棱柱
長方形
S=2S底+S側(cè)
V=S底·h
圓柱
長方形
S=2πr2+2πrl
V=πr2·l
棱錐
由若干三角形構(gòu)成
S=S底+S側(cè)
V=S底·h
圓錐
扇形
S=πr2+πrl
V=πr2·h
棱臺
由若干個梯形構(gòu)成
S=S上底+S下底+S側(cè)
V=(S++S′)·h
圓臺
扇環(huán)
S=πr′2+π(r+r′)l+πr2
V=π(r2+rr′+
2��、r′2)·h
球
S=4πr2
S=πr3
3.平行��、垂直關(guān)系的轉(zhuǎn)化示意圖
1.易混淆幾何體的表面積與側(cè)面積的區(qū)別�,幾何體的表面積是幾何體的側(cè)面積與所有底面面積之和,不能漏掉幾何體的底面積����;求錐體體積時�,易漏掉體積公式中的系數(shù).
2.不清楚空間線面平行與垂直關(guān)系中的判定定理和性質(zhì)定理,忽視判定定理和性質(zhì)定理中的條件�,導(dǎo)致判斷出錯.如由α⊥β,α∩β=l����,m⊥l,易誤得出m⊥β的結(jié)論,就是因為忽視面面垂直的性質(zhì)定理中m?α的限制條件.
3.注意圖形的翻折與展開前后變與不變的量以及位置關(guān)系.對照前后圖形���,弄清楚變與不變的元素后�����,再立足于不變的元素的位置關(guān)系與數(shù)量關(guān)
3�、系去探求變化后的元素在空間中的位置與數(shù)量關(guān)系.
1.將邊長為1的正方形以其一邊所在直線為旋轉(zhuǎn)軸旋轉(zhuǎn)一周��,所得幾何體的側(cè)面積是________.
答案 2π
解析 幾何體的底面圓半徑為1�����,高為1��,則側(cè)面積S=2πrh=2π×1×1=2π.
2.用平面α截球O所得截面圓的半徑為3���,球心O到平面α的距離為4����,則此球的表面積為__________.
答案 100π
解析 依題意��,設(shè)球的半徑為R��,滿足R2=32+42=25�����,
∴S球=4πR2=100π.
3.(2017·南京高淳區(qū)質(zhì)檢)若正四棱錐的底面邊長為2����,體積為8,則其側(cè)面積為__________.
答案 4
解析 因為V
4�、=×(2)2h=8,所以h=3����,
所以斜高h′==.
所以其側(cè)面積為S側(cè)=4×=4.
4.設(shè)m,n是不同的直線�,α,β���,γ是不同的平面�,有以下四個命題:
①?β∥γ���;②?m⊥β���;
③?α⊥β;④?m∥α.
其中正確的命題是________.(填序號)
答案 ①③
解析?���、僦衅叫杏谕黄矫娴膬善矫嫫叫惺钦_的;②中m��,β可能平行���,相交或直線在平面內(nèi)���;③中由面面垂直的判定定理可知結(jié)論正確;④中m��,α可能平行或線在面內(nèi).
5.在三棱錐S-ABC中�,底面ABC是邊長為3的等邊三角形,SA⊥SC�����,SB⊥SC����,SA=SB=2,則該三棱錐的體積為________.
答案
解析 如圖�,
5、∵SA⊥SC���,SB⊥SC����,且SA∩SB=S���,
∴SC⊥平面SAB����,
在Rt△BSC中�,由SB=2,BC=3���,得SC=.
在△SAB中��,取AB中點D����,連結(jié)SD�,則SD⊥AB,且BD=���,
∴SD==�,
∴V=××3××=.
6.已知m,n為不同直線���,α����,β為不同平面��,給出下列命題:
①若m⊥α�,m⊥n,則n∥α�;
②若m⊥β,n⊥β����,則m∥n;
③若m⊥α�����,m⊥β�����,則α∥β;
④若m?α�,n?β���,α∥β��,則n∥m�;
⑤若α⊥β�����,α∩β=m����,n?α,m⊥n����,則n⊥β.
其中正確的命題是________.(填寫所有正確命題的序號)
答案 ②③⑤
解析 命題①����,若m⊥α,
6����、m⊥n����,則n∥α或n?α�����,故不正確�;命題②,若m⊥β��,n⊥β���,則m∥n���,由線面垂直的性質(zhì)定理易知正確;命題③���,由線面垂直的性質(zhì)定理易知正確�����;命題④��,若m?α�����,n?β�,α∥β,則n∥m或m����,n異面�����,所以不正確�����;命題⑤是面面垂直的性質(zhì)定理����,所以是正確命題.故答案為②③⑤.
7.如圖,三棱錐A-BCD的棱長全相等�,點E為AD的中點,則直線CE與BD所成角的余弦值為__________.
答案
解析 方法一 取AB的中點G����,連結(jié)EG��,CG.
∵E為AD的中點���,∴EG∥BD.
∴∠GEC為CE與BD所成的角.設(shè)AB=1,
則EG=BD=�����,CE=CG=����,
∴cos∠GEC=
=
=
7、.
方法二 設(shè)AB=1����,則·=(-)·(-)=·(-)
=2-·-·+·
=-cos60°-cos60°+cos60°=.
∴cos〈,〉===.
8.如圖所示�����,在邊長為5+的正方形ABCD中���,以A為圓心畫一個扇形�,以O(shè)為圓心畫一個圓,M����,N,K為切點�����,以扇形為圓錐的側(cè)面�����,以圓O為圓錐底面��,圍成一個圓錐���,則圓錐的全面積S=________.
答案 10π
解析 設(shè)圓錐的母線長為l,底面半徑為r�����,由已知條件得
解得r=�,l=4,則S=πrl+πr2=10π.
9.如圖,在四棱錐P-ABCD中����,底面ABCD為矩形,PD⊥BC���,G為PA上一點.
(1)求證:平面PCD⊥平面A
8�、BCD�;
(2)若PC∥平面BDG,求證:G為PA的中點.
證明 (1)∵底面ABCD為矩形��,∴BC⊥CD�,
又∵PD⊥BC,PD∩CD=D���,CD��,PD?平面PCD�����,
∴BC⊥平面PCD.
又∵BC?平面ABCD�,∴平面ABCD⊥平面PCD.
(2)連結(jié)AC交BD于點O����,連結(jié)GO���,∵PC∥平面BDG,
平面PCA∩平面BDG=GO�,
∴PC∥GO,
∴=.
∵底面ABCD為矩形����,
∴O是AC的中點,即CO=OA��,
∴PG=GA�,∴G為PA的中點.
10.在正四棱錐S-ABCD中,底面邊長為a�,側(cè)棱長為a,P為側(cè)棱SD上的一點.
(1)當四面體ACPS的體積為時��,
9�����、求的值�;
(2)在(1)的條件下�,若E是SC的中點,求證:BE∥平面APC.
(1)解 設(shè)PD=x,連結(jié)BD�,AC,交點為O.過P作PH⊥BD于點H�����,∵平面SBD⊥平面ABCD且BD為交線�,則PH⊥平面ABCD,又SO⊥平面ABCD�,
∴PH∥SO.
在Rt△SOB中,SO==a�,
∵=,
∴PH===x��,
∴VSPAC=VS-ACD-VP-ACD
=×=a3�,
解得x=a,
∴==2.
(2)證明 取SP的中點Q��,連結(jié)QE�����,BQ��,
則EQ∥PC��,EQ?平面PAC,PC?平面PAC�����,
∴EQ∥平面PAC.
∵P為QD的中點���,O為BD的中點�,
∴BQ∥PO���,又BQ?平面PAC�����,PO?平面PAC�����,
∴BQ∥平面PAC�����,
而EQ與BQ為平面BEQ內(nèi)的兩條相交直線,
∴平面BEQ∥平面PAC�����,
而BE?平面BEQ,∴BE∥平面APC.
 (江蘇專用)高考數(shù)學(xué)總復(fù)習 考前三個月 考前回扣6 立體幾何 理-人教版高三數(shù)學(xué)試題
(江蘇專用)高考數(shù)學(xué)總復(fù)習 考前三個月 考前回扣6 立體幾何 理-人教版高三數(shù)學(xué)試題