《安徽省長豐縣高中數(shù)學 第三章 導數(shù)及其應用 3.2 導數(shù)的計算 3.2.1 幾個常用函數(shù)的導數(shù)教案 新人教A版選修11》由會員分享�,可在線閱讀,更多相關(guān)《安徽省長豐縣高中數(shù)學 第三章 導數(shù)及其應用 3.2 導數(shù)的計算 3.2.1 幾個常用函數(shù)的導數(shù)教案 新人教A版選修11(4頁珍藏版)》請在裝配圖網(wǎng)上搜索�。
1、
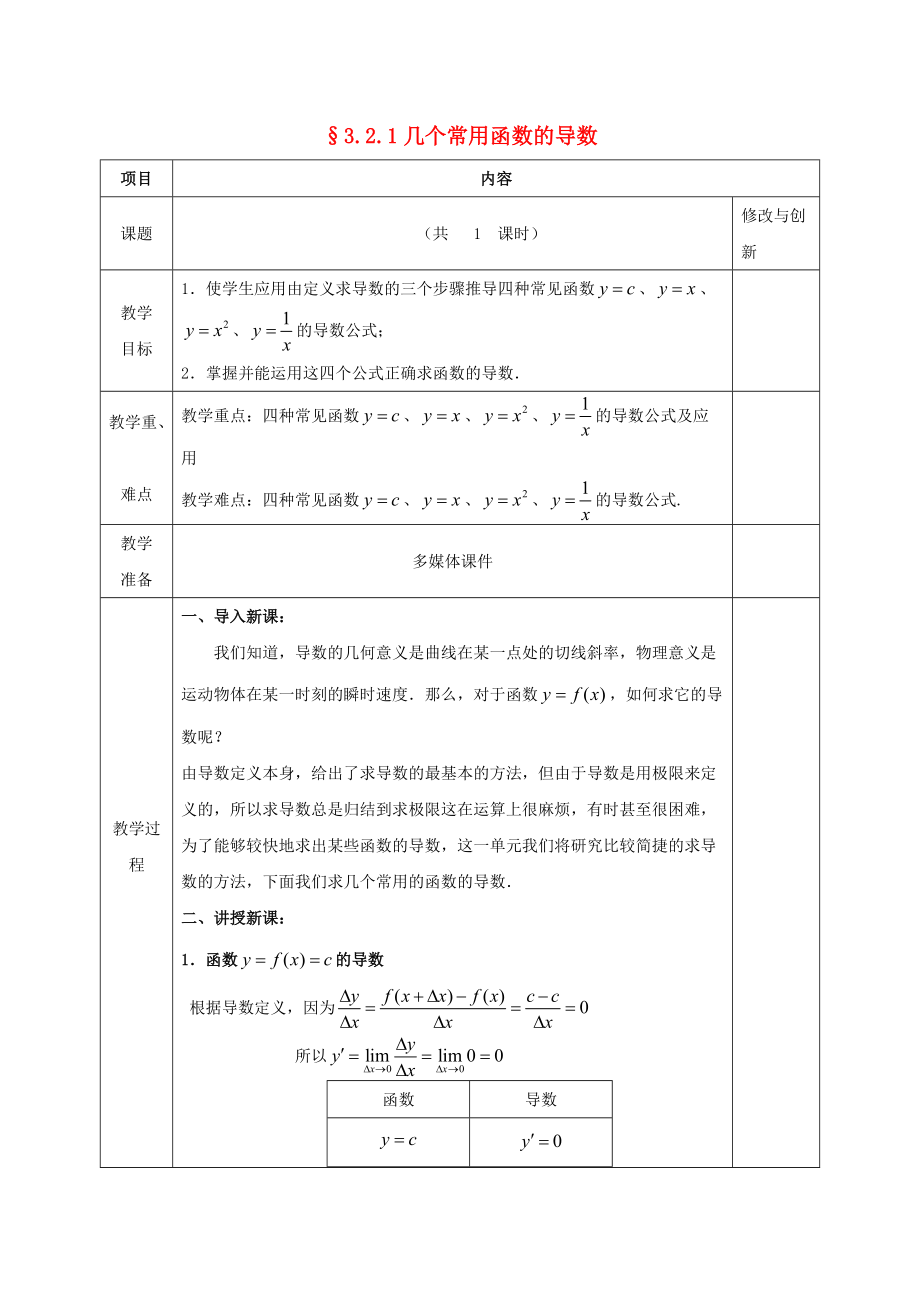
3.2.1幾個常用函數(shù)的導數(shù)
項目
內(nèi)容
課題
(共 1 課時)
修改與創(chuàng)新
教學
目標
1.使學生應用由定義求導數(shù)的三個步驟推導四種常見函數(shù)����、、����、的導數(shù)公式;
2.掌握并能運用這四個公式正確求函數(shù)的導數(shù).
教學重�����、
難點
教學重點:四種常見函數(shù)�、、����、的導數(shù)公式及應用
教學難點:四種常見函數(shù)、���、��、的導數(shù)公式.
教學
準備
多媒體課件
教學過程
一�����、導入新課:
我們知道����,導數(shù)的幾何意義是曲線在某一點處的切線斜率,物理意義是運動物體在某一時刻的瞬時速度.那么�,對于函數(shù),如何求它的導數(shù)呢��?
由導數(shù)定義本身��,給出了求導數(shù)的最基本的
2����、方法���,但由于導數(shù)是用極限來定義的���,所以求導數(shù)總是歸結(jié)到求極限這在運算上很麻煩����,有時甚至很困難����,為了能夠較快地求出某些函數(shù)的導數(shù),這一單元我們將研究比較簡捷的求導數(shù)的方法��,下面我們求幾個常用的函數(shù)的導數(shù).
二�、講授新課:
1.函數(shù)的導數(shù)
根據(jù)導數(shù)定義,因為
所以
函數(shù)
導數(shù)
表示函數(shù)圖像(圖3.2-1)上每一點處的切線的斜率都為0.若表示路程關(guān)于時間的函數(shù)��,則可以解釋為某物體的瞬時速度始終為0��,即物體一直處于靜止狀態(tài).
2.函數(shù)的導數(shù)
因為
所以
函數(shù)
導數(shù)
表示函數(shù)圖像(圖3.2-2)上每一點處的切線的斜率都為1.若表示路程關(guān)于時間的函數(shù)�,則可以解釋
3、為某物體做瞬時速度為1的勻速運動.
3.函數(shù)的導數(shù)
因為
所以
函數(shù)
導數(shù)
表示函數(shù)圖像(圖3.2-3)上點處的切線的斜率都為��,說明隨著的變化���,切線的斜率也在變化.另一方面�����,從導數(shù)作為函數(shù)在一點的瞬時變化率來看�,表明:當時,隨著的增加�,函數(shù)減少得越來越慢;當時��,隨著的增加�����,函數(shù)增加得越來越快.若表示路程關(guān)于時間的函數(shù)�����,則可以解釋為某物體做變速運動���,它在時刻的瞬時速度為.
4.函數(shù)的導數(shù)
因為
所以
函數(shù)
導數(shù)
5.函數(shù)的導數(shù)
因為
所以
函數(shù)
導數(shù)
(2)推廣:若��,則
三.課堂練習
1.課本P13探究1
2.課本P13
4����、探究2
課堂小結(jié):
函數(shù)
導數(shù)
布置作業(yè):
P85. 1,2,3
板書設(shè)計
3.2.1幾個常用函數(shù)的導數(shù)
1.函數(shù)的導數(shù)
2.函數(shù)的導數(shù)
3.函數(shù)的導數(shù)
4.函數(shù)的導數(shù)
5.函數(shù)的導數(shù)
教學反思
用導函數(shù)定義可以求常見函數(shù)的導數(shù)���,但由于相關(guān)極限知識中學教材已刪減,所以只能對常數(shù)函數(shù)和幾個簡單的冪函數(shù)按定義求它們的導函數(shù)����,所以教學中�����,讓學生自己由定義求所給幾個冪函數(shù)的導數(shù)���,教師必要時給與指導。
6EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F375
 安徽省長豐縣高中數(shù)學 第三章 導數(shù)及其應用 3.2 導數(shù)的計算 3.2.1 幾個常用函數(shù)的導數(shù)教案 新人教A版選修11
安徽省長豐縣高中數(shù)學 第三章 導數(shù)及其應用 3.2 導數(shù)的計算 3.2.1 幾個常用函數(shù)的導數(shù)教案 新人教A版選修11