《人教版高中數(shù)學(xué)必修二檢測(cè):第一章 空間幾何體 課后提升作業(yè) 五 1.3.1含解析》由會(huì)員分享�����,可在線閱讀�����,更多相關(guān)《人教版高中數(shù)學(xué)必修二檢測(cè):第一章 空間幾何體 課后提升作業(yè) 五 1.3.1含解析(9頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�。
1、
人教版高中數(shù)學(xué)必修精品教學(xué)資料
課后提升作業(yè)五
柱體、錐體��、臺(tái)體的表面積與體積
(45分鐘 70分)
一�����、選擇題(每小題5分,共40分)
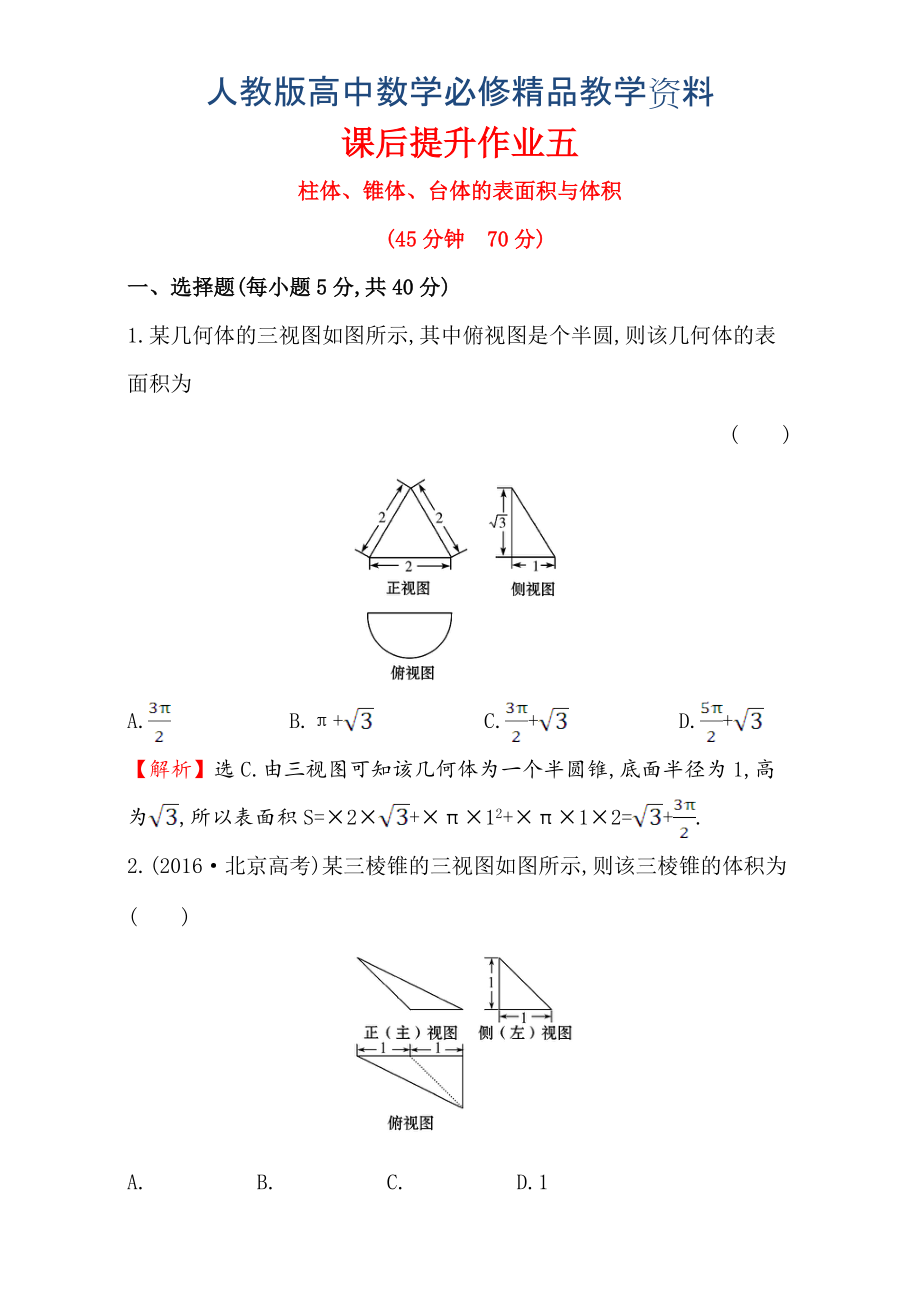
1.某幾何體的三視圖如圖所示,其中俯視圖是個(gè)半圓,則該幾何體的表面積為
( )
A. B.π+ C.+ D.+
【解析】選C.由三視圖可知該幾何體為一個(gè)半圓錐,底面半徑為1,高為,所以表面積S=2+π12+π12=+.
2.(2016北京高考)某三棱錐的三視圖如圖所示,則該三棱錐的體積為 ( )
A. B. C. D.1
【解析】選A.通過(guò)三視圖可還原幾何體為如圖所示的三棱錐,
2�、則通過(guò)側(cè)視圖得高h(yuǎn)=1,底面積S=11=,所以體積V=Sh=.
3.(2016太原高一檢測(cè))如圖,正方體ABCD-A′B′C′D′的棱長(zhǎng)為4,動(dòng)點(diǎn)E,F在棱AB上,且EF=2,動(dòng)點(diǎn)Q在棱D′C′上,則三棱錐A′-EFQ的體積 ( )
.Com]
A.與點(diǎn)E,F的位置有關(guān)
B.與點(diǎn)Q的位置有關(guān)
C.與點(diǎn)E,F,Q的位置都有關(guān)
D.與點(diǎn)E,F,Q的位置均無(wú)關(guān),是定值
【解析】選D.VA′-EFQ=VQ-A′EF=EFAA′A′D′,所以其體積為定值,與點(diǎn)E,F,Q的位置均無(wú)關(guān).
4.(2016邯鄲高二檢測(cè))已知某空間幾何體的三視圖如圖所示,則該幾何體的體積是 ( )
3、A.16 B.24 C.32 D.48
【解析】選D.由三視圖知,該幾何體是一個(gè)四棱錐E-ABCD,底面ABCD是一個(gè)直角梯形,各邊長(zhǎng)如圖所示,BC⊥AB,EB⊥底面ABCD,AB=6,所以由棱錐的體積公式得,V=(6+2)66=48.
5.(2016山東高考)一個(gè)由半球和四棱錐組成的幾何體,其三視圖如圖所示.則該幾何體的體積為 ( )
A.+π B.+π
C.+π D.1+π
【解析】選C.由三視圖可知,半球的半徑為,四棱錐底面正方形邊長(zhǎng)為1,高為1,所以該組合體的體積=π+111=+π.
6.某幾何體的三視圖如圖所示,則它的體積是
4�����、 ( )
A.8-π B.8-π C.8-2π D.π
【解析】選A.這個(gè)幾何體是一個(gè)棱長(zhǎng)為2的正方體中挖去一個(gè)圓錐,這個(gè)圓錐的高為2,底面半徑為1,故這個(gè)幾何體體積為23-π122=8-π.
【延伸探究】本題條件不變,求該幾何體的表面積.
【解析】這個(gè)幾何體是一個(gè)棱長(zhǎng)為2的正方體中挖去一個(gè)圓錐,這個(gè)圓錐的高為2,底面半徑為1,可求得圓錐的母線l==.所以該幾何體的表面積為S表=522+22-π12+π1
=24-π+π=24+(-1)π.
7.某幾何體的三視圖如圖所示,則該幾何體的表面積為 ( )
A.180 B.200 C.220
5���、 D.240
【解析】選D.由三視圖可知該幾何體為底面為梯形的直四棱柱.底面積為2(8+2)4=40,由三視圖知,梯形的腰為=5,梯形的周長(zhǎng)為8+2+5+5=20,所以四棱柱的側(cè)面積為2010=200,表面積為240.
8.如圖為某幾何體的三視圖,則該幾何體的表面積為 ( )
A.10+ B.10+
C.6+2+ D.6++
【解析】選C.由三視圖知四邊形ABCD為直角梯形,其面積為S1==3.三角形PAB為直角三角形,其面積為S2=21=1.
三角形PAD面積為S3=22=2,PD=2,
三角形PDC面積為S4=22=2.
又PB=BC=,PC=
6�、2,作BE⊥PC于E,
則BE===,
所以三角形PBC的面積為S5=2=,
故表面積為S=S1+S2+S3+S4+S5=6+2+.
二�、填空題(每小題5分,共10分)
9.(2016寧波高二檢測(cè))若如圖為某直三棱柱(側(cè)棱與底面垂直)被削去一部分后的直觀圖與三視圖中的側(cè)視圖、俯視圖,則其正視圖的面積為_(kāi)_______,三棱錐D-BCE的體積為_(kāi)_______.
【解析】根據(jù)題意分析可知,正視圖為兩條直角邊分別是2,4的直角三角形,所以S=24=4,
VD-BCE=VB-DCE=422=.
答案:4
10.(2015天津高考)一個(gè)幾何體的三視圖如圖所示(單位:m),則該幾
7���、何體的體積為_(kāi)_______m3.
【解析】由三視圖可知,該幾何體是中間為一個(gè)底面半徑為1,高為2的圓柱,兩端是底面半徑為1,高為1的圓錐,所以該幾何體的體積V=12π2+212π1=π(m3).
答案:π
三��、解答題(每小題10分,共20分)
11.(2016鄭州高二檢測(cè))若某幾何體的三視圖(單位:cm)如圖所示,
(1)求此幾何體的表面積.
(2)求此幾何體的體積.
【解析】(1)由題意知,該幾何體是一個(gè)組合體,上邊是長(zhǎng)方體,長(zhǎng)為4cm,寬為4cm,高為2cm,下邊是一個(gè)四棱臺(tái),上底邊長(zhǎng)為4cm,下底邊長(zhǎng)為8cm,高是3cm,四棱臺(tái)的斜高為=,則該幾何體的表面積S=4
8����、4+424+88+(4+8)24=(112+24)cm2.
(2)該幾何體的體積V=442+(42+82+48)3=144(cm3).
12.如圖所示,在長(zhǎng)方體ABCD-A′B′C′D′中,用截面截下一個(gè)棱錐D′-A′DC,求棱錐D′-A′DC的體積與剩余部分的體積之比.
【解析】設(shè)AB=a,AD=b,DD′=c,
則長(zhǎng)方體ABCD-A′B′C′D′的體積V=abc,因?yàn)閂三棱錐D′-A′DC=V三棱錐C-A′DD′,
又S△A′DD′=bc,且三棱錐C-A′DD′的高為CD=a.
所以V三棱錐C-A′DD′=S△A′DD′CD=abc.
則剩余部分幾何體的體積V剩=abc-
9、abc=abc.
故V三棱錐D′-A′DC∶V剩=abc∶abc=1∶5.
【一題多解】已知長(zhǎng)方體可以看成側(cè)棱垂直于底面的四棱柱ADD′A′-
BCC′B′,設(shè)它的底面ADD′A′面積為S,高為h,則它的體積為V=Sh.因?yàn)?
V三棱錐D′-A′DC=V三棱錐C-A′DD′,
而棱錐C-A′DD′的底面面積為S,高為h,
因此棱錐C-A′DD′的體積VC-A′DD′=Sh=Sh.余下的體積是Sh-Sh=Sh.
所以棱錐C-A′DD′,即棱錐D′-A′DC的體積與剩余部分的體積之比為Sh∶Sh=1∶5.
【能力挑戰(zhàn)題】
如圖,正三棱錐O-ABC的底面邊長(zhǎng)為2,高為1,求該三棱錐的體積及表面積.
【解析】由已知條件可知,正三棱錐O-ABC的底面△ABC是邊長(zhǎng)為2的正三角形,
經(jīng)計(jì)算得底面△ABC的面積為.
所以該三棱錐的體積為1=.
設(shè)O′是正三角形ABC的中心.
由正三棱錐的性質(zhì)可知,OO′⊥平面ABC.
延長(zhǎng)AO′交BC于D,連接OD,得AD=,O′D=.
又因?yàn)镺O′=1,所以正三棱錐的斜高OD=.
故側(cè)面積為32=2.
所以該三棱錐的表面積為+2=3,
因此,所求三棱錐的體積為,表面積為3.
關(guān)閉Word文檔返回原板塊
 人教版高中數(shù)學(xué)必修二檢測(cè):第一章 空間幾何體 課后提升作業(yè) 五 1.3.1含解析
人教版高中數(shù)學(xué)必修二檢測(cè):第一章 空間幾何體 課后提升作業(yè) 五 1.3.1含解析