精校版高中數(shù)學(xué) 第2章 第12課時(shí) 直線與平面垂直的判定課時(shí)作業(yè) 人教A版必修2

《精校版高中數(shù)學(xué) 第2章 第12課時(shí) 直線與平面垂直的判定課時(shí)作業(yè) 人教A版必修2》由會員分享，可在線閱讀，更多相關(guān)《精校版高中數(shù)學(xué) 第2章 第12課時(shí) 直線與平面垂直的判定課時(shí)作業(yè) 人教A版必修2（5頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

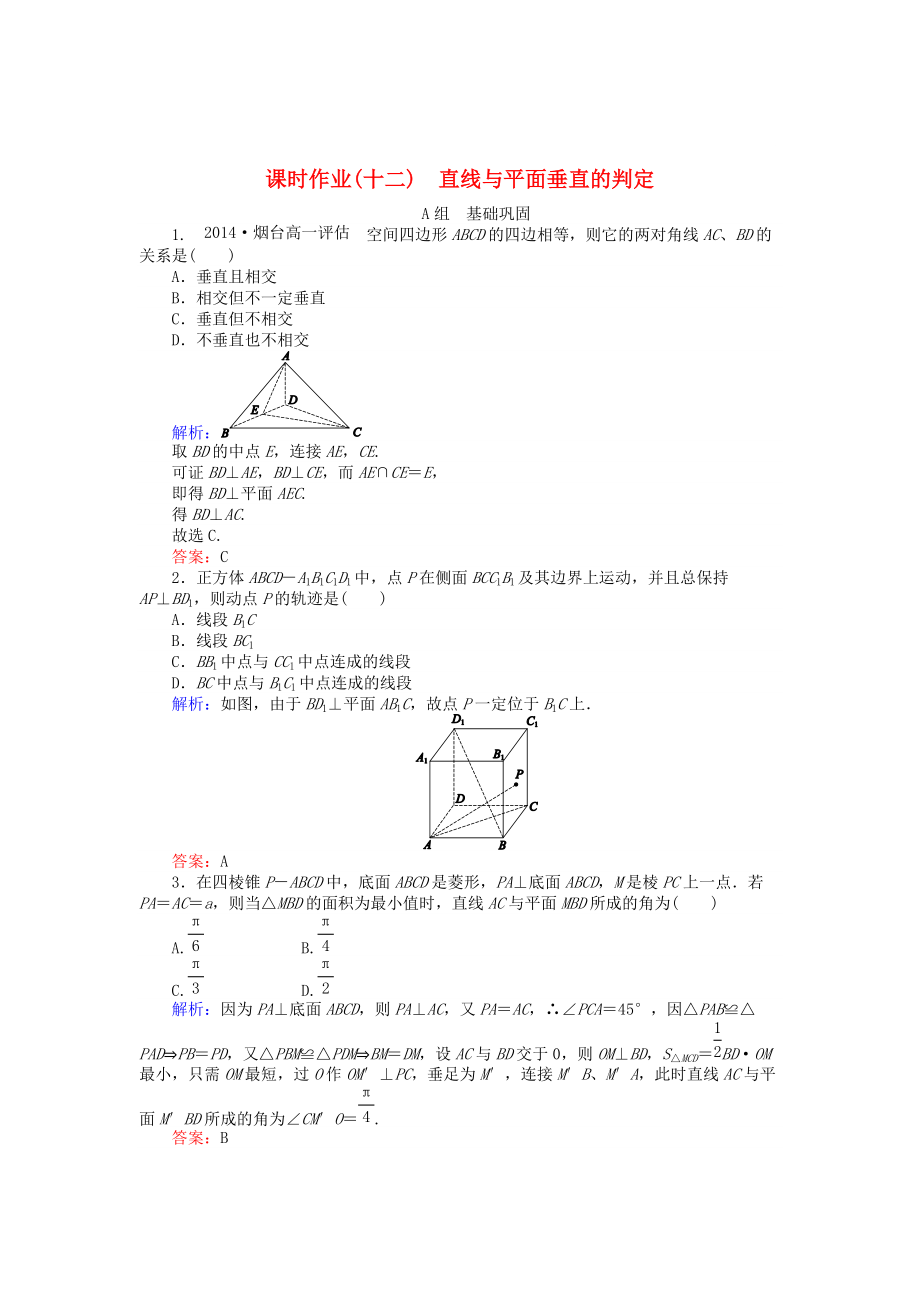
1、最新資料最新資料最新資料最新資料最新資料 課時(shí)作業(yè)(十二)　直線與平面垂直的判定 A組　基礎(chǔ)鞏固 1.空間四邊形ABCD的四邊相等，則它的兩對角線AC、BD的關(guān)系是(　　) A．垂直且相交 B．相交但不一定垂直 C．垂直但不相交 D．不垂直也不相交 解析： 取BD的中點(diǎn)E，連接AE，CE. 可證BD⊥AE，BD⊥CE，而AE∩CE＝E， 即得BD⊥平面AEC. 得BD⊥AC. 故選C. 答案：C 2．正方體ABCD－A1B1C1D1中，點(diǎn)P在側(cè)面BCC1B1及其邊界上運(yùn)動，并且總保持AP⊥BD1，則動點(diǎn)P的軌跡是(　　) A．線段B1C B．線段BC1 C．

2、BB1中點(diǎn)與CC1中點(diǎn)連成的線段 D．BC中點(diǎn)與B1C1中點(diǎn)連成的線段 解析：如圖，由于BD1⊥平面AB1C，故點(diǎn)P一定位于B1C上． 答案：A 3．在四棱錐P－ABCD中，底面ABCD是菱形，PA⊥底面ABCD，M是棱PC上一點(diǎn)．若PA＝AC＝a，則當(dāng)△MBD的面積為最小值時(shí)，直線AC與平面MBD所成的角為(　　) A.　　　　　　B. C. D. 解析：因?yàn)镻A⊥底面ABCD，則PA⊥AC，又PA＝AC，∴∠PCA＝45，因△PAB≌△PAD?PB＝PD，又△PBM≌△PDM?BM＝DM，設(shè)AC與BD交于0，則OM⊥BD，S△MCD＝BDOM最小，只

3、需OM最短，過O作OM′⊥PC，垂足為M′，連接M′B、M′A，此時(shí)直線AC與平面M′BD所成的角為∠CM′O＝. 答案：B 4．如圖，四棱錐P－ABCD中，PA⊥平面ABCD，則PD與平面ABCD所成的角為圖中的(　　) A．∠PAD B．∠PDA C．∠PDB D．∠PDC 解析：∵PA⊥平面ABCD，∴AD是PD在平面ABCD上的射影，故∠PDA是PD與平面ABCD所成的角． 答案：B 5．若斜線段AB是它在平面α內(nèi)的射影長的2倍，則AB與平面α所成角為(　　) A．30 B．45 C．60 D．120 解析：設(shè)AB與平面α所成的角為θ，由題意可知cosθ

4、＝，∴θ＝60. 答案：C 6．已知三條相交于點(diǎn)P的線段PA，PB，PC兩兩垂直，P在平面ABC外，PH⊥平面ABC于H，則垂足H是三角形ABC的(　　) A．外心 B．內(nèi)心 C．垂心 D．重心 解析：如圖，∵PA、PB、PC兩兩垂直，∴PA⊥平面PBC， ∴PA⊥BC. 又BC⊥PH，PA∩PH＝P， ∴BC⊥平面PAH，∴BC⊥AH. 同理AB⊥CH，AC⊥BH. ∴點(diǎn)H為△ABC的垂心． 答案：C 7．如圖，△ADB和△ADC都是以D為直角頂點(diǎn)的直角三角形，且AD＝BD＝CD，∠BAC＝60，則直線AD⊥平面________；直線BD⊥平面______

5、__；直線CD⊥平面________． 解析：∵△ADB、△ADC都是直角三角形， ∴AD⊥BD，AD⊥DC， 又BD∩DC＝D， ∴AD⊥平面BDC. 又AD＝BD＝CD，∴AB＝AC， 又∠BAC＝60， ∴△ABC為正三角形， ∴BC＝AB＝AC， ∴∠BDC＝90， 由直線和平面垂直的判定定理， 得BD⊥平面ADC，CD⊥平面ABD. 答案：BDC　ADC　ABD 8．在Rt△ABC中，D是斜邊AB的中點(diǎn)，AC＝6，BC＝8，EC⊥平面ABC，且EC＝12，則ED＝________. 解析： 如圖所示，在Rt△ABC中，CD＝AB. ∵AC＝6，BC＝8

6、， ∴AB＝＝10. ∴CD＝5. ∵EC⊥平面ABC，CD?平面ABC， ∴EC⊥CD. ∴ED＝＝＝13. 答案：13 9．如圖所示：直角△ABC所在的平面外一點(diǎn)S，SA＝SB＝SC，點(diǎn)D為斜邊AC的中點(diǎn)．則直線SD與平面ABC的位置關(guān)系為________． 解析：∵SA＝SC，點(diǎn)D為斜邊AC的中點(diǎn)， ∴SD⊥AC. 則在Rt△ABC中，AD＝DC＝BD， ∴△ADS≌△BDS， ∴SD⊥BD.又AC∩BD＝D，∴SD⊥平面ABC. 答案：垂直 10．如圖，四棱錐P－ABCD的底面是邊長為1的正方形，PD⊥BC，PD＝1，PC＝. 求證：PD⊥平面AB

7、CD. 證明：∵PD＝DC＝1，PC＝， ∴PD2＋DC2＝PC2， ∴△PDC是直角三角形． ∴PD⊥CD. 又∵PD⊥BC，BC∩CD＝C，且BC?平面ABCD，CD?平面ABCD，∴PD⊥平面ABCD. B組　能力提升 11．在正方體ABCD－A1B1C1D1中，E，F(xiàn)分別是AA1，A1D1的中點(diǎn)，求： (1)D1B與平面ABCD所成角的余弦值； (2)EF與平面A1B1C1D1所成的角． 解析：(1)如圖所示，連接DB， ∵D1D⊥平面ABCD， ∴DB是D1B在平面ABCD內(nèi)的射影． 則∠D1BD即為D1B與平面ABCD所成的角． ∵DB＝AB，D

8、1B＝AB， ∴cos∠D1BD＝＝， 即D1B與平面ABCD所成角的余弦值為. (2)∵E是A1A的中點(diǎn)，A1A⊥平面A1B1C1D1， ∴∠EFA1是EF與平面A1B1C1D1所成的角． 在Rt△EA1F中，∵F是A1D1的中點(diǎn)， ∴∠EFA1＝45. 12．如圖，在四棱錐P－ABCD中，底面ABCD為平行四邊形，∠ADC＝45，AD＝AC＝1，O為AC的中點(diǎn)，PO⊥平面ABCD，PO＝2，M為PD的中點(diǎn)． (1)證明：PB∥平面ACM； (2)證明：AD⊥平面PAC； (3)求直線AM與平面ABCD所成角的正切值． 解析： (1)證明：如圖連接BD，MO.

9、在平行四邊形ABCD中， ∵O為AC的中點(diǎn)， ∴O為BD的中點(diǎn)， 又M為PD的中點(diǎn)， ∴PB∥MO. ∵PB?平面ACM，MO?平面ACM， ∴PB∥平面ACM. (2)證明：∵∠ADC＝45，且AD＝AC＝1， ∴∠DAC＝90，即AD⊥AC. 又PO⊥平面ABCD，AD?平面ABCD， ∴PO⊥AD，而AC∩PO＝O，∴AD⊥平面PAC. (3)解：取DO的中點(diǎn)N，連接MN，AN. ∵M(jìn)為PD的中點(diǎn)， ∴MN∥PO，且MN＝PO＝1. 由PO⊥平面ABCD，得MN⊥平面ABCD， ∴∠MAN是直線AM與平面ABCD所成的角． 在Rt△DAO中，AD＝1，AO＝，∴DO＝， 從而AN＝DO＝. 在Rt△ANM中，tan∠MAN＝＝＝， 即直線AM與平面ABCD所成角的正切值為. 最新精品資料