《2018-2019學(xué)年九年級數(shù)學(xué)下冊 第二十七章 相似本章中考演練同步練習(xí) (新版)新人教版》由會員分享����,可在線閱讀,更多相關(guān)《2018-2019學(xué)年九年級數(shù)學(xué)下冊 第二十七章 相似本章中考演練同步練習(xí) (新版)新人教版(8頁珍藏版)》請在裝配圖網(wǎng)上搜索���。
1�、
第二十七章 相似
一、選擇題
1.2018·內(nèi)江已知△ABC與△A1B1C1相似����,且相似比為1∶3,則△ABC與△A1B1C1的面積比為( )
A.1∶1 B.1∶3
C.1∶6 D.1∶9
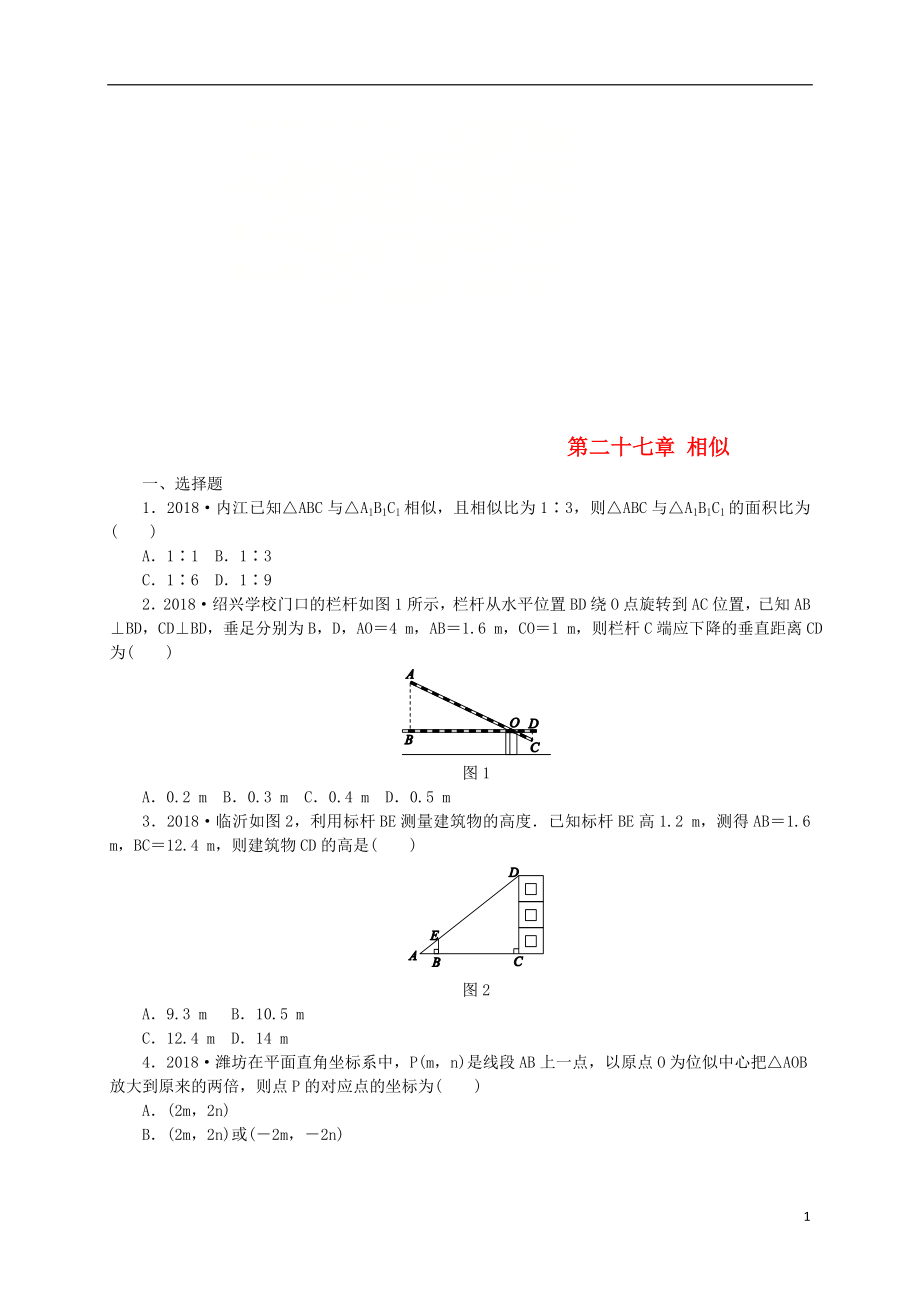
2.2018·紹興學(xué)校門口的欄桿如圖1所示��,欄桿從水平位置BD繞O點旋轉(zhuǎn)到AC位置����,已知AB⊥BD,CD⊥BD��,垂足分別為B���,D����,AO=4 m�����,AB=1.6 m���,CO=1 m�,則欄桿C端應(yīng)下降的垂直距離CD為( )
圖1
A.0.2 m B.0.3 m C.0.4 m D.0.5 m
3.2018·臨沂如圖2,利用標(biāo)桿BE測量建筑物的高度.已知標(biāo)桿BE高1.2
2��、 m�,測得AB=1.6 m�,BC=12.4 m,則建筑物CD的高是( )
圖2
A.9.3 m B.10.5 m
C.12.4 m D.14 m
4.2018·濰坊在平面直角坐標(biāo)系中����,P(m,n)是線段AB上一點����,以原點O為位似中心把△AOB放大到原來的兩倍,則點P的對應(yīng)點的坐標(biāo)為( )
A.(2m�,2n)
B.(2m,2n)或(-2m����,-2n)
C.(m,n)
D.(m��,n)或(-m��,-n)
5.2018·宜賓如圖3,將△ABC沿BC邊上的中線AD平移到△A′B′C′的位置����,已知△ABC的面積為9,陰影部分三角形的面積為4.若AA′=1�����,則A′D等于( )
3�、
圖3
A.2 B.3 C. D.
6.2018·泰州如圖4,平面直角坐標(biāo)系xOy中�����,點A的坐標(biāo)為(9�,6),AB⊥y軸��,垂足為B�,點P從原點O出發(fā)向x軸正方向運動,同時����,點Q從點A出發(fā)向點B運動,當(dāng)點Q到達(dá)點B時�,點P����,Q同時停止運動��,若點P與點Q的速度之比為1∶2����,則下列說法正確的是( )
圖4
A.線段PQ始終經(jīng)過點(2�����,3)
B.線段PQ始終經(jīng)過點(3�,2)
C.線段PQ始終經(jīng)過點(2,2)
D.線段PQ不可能始終經(jīng)過某一定點
二�����、填空題
7.2018·嘉興如圖5�,直線l1∥l2∥l3,直線AC分別交l1�����,l2��,l3于點A,B��,C��,直線DF分別交l1
4�、,l2����,l3于點D,E����,F(xiàn),已知=�����,則=________.
圖5
8.2018·南充如圖6��,在△ABC中���,DE∥BC�����,BF平分∠ABC���,交DE的延長線于點F�����,若AD=1���,BD=2,BC=4���,則EF=________.
圖6
9.2018·岳陽《九章算術(shù)》是我國古代數(shù)學(xué)名著,書中有下列問題:“今有勾五步�,股十二步,問勾中容方幾何����?”其意思為:“如圖7,今有直角三角形��,勾(短直角邊)長為5步����,股(長直角邊)長為12步���,問該直角三角形能容納的正方形邊長最大是多少步?”該問題的答案是________步.
圖7
三��、解答題
10.2018·杭州如圖8�����,在△ABC中��,AB=AC
5��、�,AD為BC邊上的中線,DE⊥AB于點E.
(1)求證:△BDE∽△CAD�����;
(2)若AB=13��,BC=10����,求線段DE的長.
圖8
11.2018·安徽如圖9,在由邊長為1個單位長度的小正方形組成的10×10網(wǎng)格中�����,已知點O,A����,B均為網(wǎng)格線的交點.
(1)在給定的網(wǎng)格中,以點O為位似中心����,將線段AB放大為原來的2倍,得到線段A1B1(點A����,B的對應(yīng)點分別為A1,B1)�����,畫出線段A1B1���;
(2)將線段A1B1繞點B1逆時針旋轉(zhuǎn)90°得到線段A2B1,畫出線段A2B1�;
(3)以A,A1�,B1�,A2為頂點的四邊形AA1B1A2的面積是__
6����、______個平方單位.
圖9
12.2018·衢州如圖10,已知AB為⊙O的直徑���,AC是⊙O的切線��,連接BC交⊙O于點F�����,取的中點D�,連接AD交BC于點E��,過點E作EH⊥AB于點H.
(1)求證:△HBE∽△ABC����;
(2)若CF=4,BF=5����,求AC和EH的長.
圖10
13.2018·寧波若一個三角形一條邊的平方等于另兩條邊的乘積,我們把這個三角形叫做比例三角形.
(1)已知△ABC是比例三角形,AB=2����,BC=3,請直接寫出所有滿足條件的AC的長�����;
(2)如圖11①����,在四邊形ABCD中,AD∥BC��,對角線BD平分∠AB
7��、C�,∠BAC=∠ADC.求證:△ABC是比例三角形;
(3)如圖②����,在(2)的條件下�����,當(dāng)∠ADC=90°時�����,求的值.
圖11
詳解詳析
1.[解析] D ∵△ABC與△A1B1C1相似,且相似比為1∶3��,∴=()2=.故選D.
2.[解析] C 由題意可知△ABO∽△CDO����,根據(jù)相似三角形的性質(zhì)可得=,又AO=4 m�,AB=1.6 m,CO=1 m���,∴=�����,解得CD=0.4(m).故選C.
3.[解析] B 由題意知BE∥CD�,∴△ABE∽△ACD���,∴=�,即=�,解得CD=10.5(m).故選B.
4.[解析] B 當(dāng)放大后的△A′O′B′與△AOB在原點O的同側(cè)時,點P
8、的對應(yīng)點的坐標(biāo)為(2m�,2n);當(dāng)放大后的△A′O′B′與△AOB在原點O的異側(cè)時����,點P的對應(yīng)點的坐標(biāo)為(-2m,-2n).故選B.
5.[解析] A 如圖��,∵S△ABC=9����,S△A′EF=4,且AD為BC邊上的中線����,
∴S△A′DE=S△A′EF=2,S△ABD=S△ABC=.
∵將△ABC沿BC邊上的中線AD平移得到△A′B′C′�,
∴A′E∥AB,
∴△DA′E∽△DAB����,∴=,
即=�����,
解得A′D=2或A′D=-(舍去).故選A.
6.[解析] B 解法一:如圖�����,連接AO交PQ于點C�����,過點C作CD⊥AB于點D���,
∵AB⊥y軸����,
∴AB∥x軸����,
∴∠A=∠COP
9、�����,∠AQC=∠OPC��,
∴△AQC∽△OPC��,
∴==2,
∴=.
同理可得CD=BO=4�����,AD=AB=6.
∵點A的坐標(biāo)為(9���,6)����,
∴點C的坐標(biāo)為(3��,2).
即線段PQ始終經(jīng)過點(3���,2).故選B.
解法二:當(dāng)OP=t時��,點P的坐標(biāo)為(t�����,0)�,點Q的坐標(biāo)為(9-2t�,6).
設(shè)直線PQ的解析式為y=kx+b(k≠0),
將P(t�����,0),Q(9-2t����,6)代入y=kx+b��,
得解得
∴直線PQ的解析式為y=x+.
當(dāng)x=3時�,y=2,
∴直線PQ始終經(jīng)過點(3����,2).
故選B.
7.[答案] 2
[解析] 由=得==,則=2.
因為直線l1∥l2
10��、∥l3����,所以==2.
故答案為2.
8.[答案]
[解析] ∵DE∥BC,AD=1�����,BD=2�����,BC=4,∴=�,即=,解得DE=.∵BF平分∠ABC��,∴∠ABF=∠FBC.又∵DE∥BC��,∴∠FBC=∠F����,∴∠ABF=∠F,∴BD=DF=2.∵DF=DE+EF��,∴EF=2-=.故答案為:.
9.[答案]
[解析] 如圖.
設(shè)該直角三角形能容納的正方形邊長為x��,則AD=12-x�����,F(xiàn)C=5-x.
根據(jù)題意����,得△ADE∽△EFC,
∴=�,
即=��,解得x=.
故答案為.
10.解:(1)證明:∵AB=AC��,∴∠ABC=∠ACB.
∵AB=AC�����,AD是BC邊上的中線����,∴BD
11�、=CD�,AD⊥BC.
又∵DE⊥AB,∴∠DEB=∠ADC��,
∴△BDE∽△CAD.
(2)∵BC=10���,∴BD=BC=5.
在Rt△ABD中�����,有AD2+BD2=AB2���,
∴AD==12.
∵△BDE∽△CAD����,∴=���,即=�����,∴DE=.
11.解:(1)如圖所示���,線段A1B1即為所求.
(2)如圖所示,線段A2B1即為所求.
(3)由圖可得�����,四邊形AA1B1A2為正方形�,
∴四邊形AA1B1A2的面積是()2=()2=20.
故答案為:20.
12.[解析] (1)根據(jù)切線的性質(zhì)可證明∠CAB=∠EHB,由此即可解決問題���;
(2)連接AF.由△CAF∽△CBA����,推出
12、AC2=CF·CB=36���,可得AC=6���,AB==3 ,AF==2 �,由Rt△AEF≌Rt△AEH,推出AF=AH=2 .設(shè)EF=EH=x.在Rt△EHB中���,可得(5-x)2=x2+()2�,解方程即可解決問題.
解:(1)證明:∵AC是⊙O的切線��,∴CA⊥AB.
∵EH⊥AB���,∴∠EHB=∠CAB.
又∵∠EBH=∠CBA,∴△HBE∽△ABC.
(2)如圖����,連接AF.
∵AB是⊙O的直徑,∴∠AFB=90°.
∵∠C=∠C��,∠CAB=∠AFC�����,
∴△CAF∽△CBA,∴=����,
∴AC2=CF·CB=36,
∴AC=6�,AB==3 ,AF==2 .
∵=���,∴∠EAF=∠EA
13����、H.
∵EF⊥AF����,EH⊥AB,∴EF=EH.
又∵AE=AE�,∴Rt△AEF≌Rt△AEH,
∴AF=AH=2 .設(shè)EF=EH=x.
在Rt△EHB中��,(5-x)2=x2+()2�,
∴x=2,∴EH=2.
13.解:(1)AC的長為或或.
(2)證明:∵AD∥BC���,
∴∠ACB=∠CAD.
又∵∠BAC=∠ADC����,
∴△ABC∽△DCA,
∴=�,即CA2=BC·AD.
∵AD∥BC,
∴∠ADB=∠CBD.
∵BD平分∠ABC���,
∴∠ABD=∠CBD�,
∴∠ADB=∠ABD�����,
∴AB=AD�,
∴CA2=BC·AB,
∴△ABC是比例三角形.
(3)如圖��,過點A作AH⊥BD于點H.
∵AB=AD�,
∴BH=BD.
∵AD∥BC�����,∠ADC=90°�����,
∴∠BCD=90°,
∴∠BHA=∠BCD=90°.
又∵∠ABH=∠DBC����,
∴△ABH∽△DBC,
∴=�����,
∴AB·BC=DB·BH�,
∴AB·BC=BD2.
又∵AB·BC=AC2,
∴BD2=AC2�����,
∴=.
8
 2018-2019學(xué)年九年級數(shù)學(xué)下冊 第二十七章 相似本章中考演練同步練習(xí) (新版)新人教版
2018-2019學(xué)年九年級數(shù)學(xué)下冊 第二十七章 相似本章中考演練同步練習(xí) (新版)新人教版