《(淄博地區(qū))2018中考數(shù)學(xué)總復(fù)習(xí) 專題八 閱讀理解試題》由會員分享��,可在線閱讀�,更多相關(guān)《(淄博地區(qū))2018中考數(shù)學(xué)總復(fù)習(xí) 專題八 閱讀理解試題(7頁珍藏版)》請在裝配圖網(wǎng)上搜索。
1���、
閱讀理解
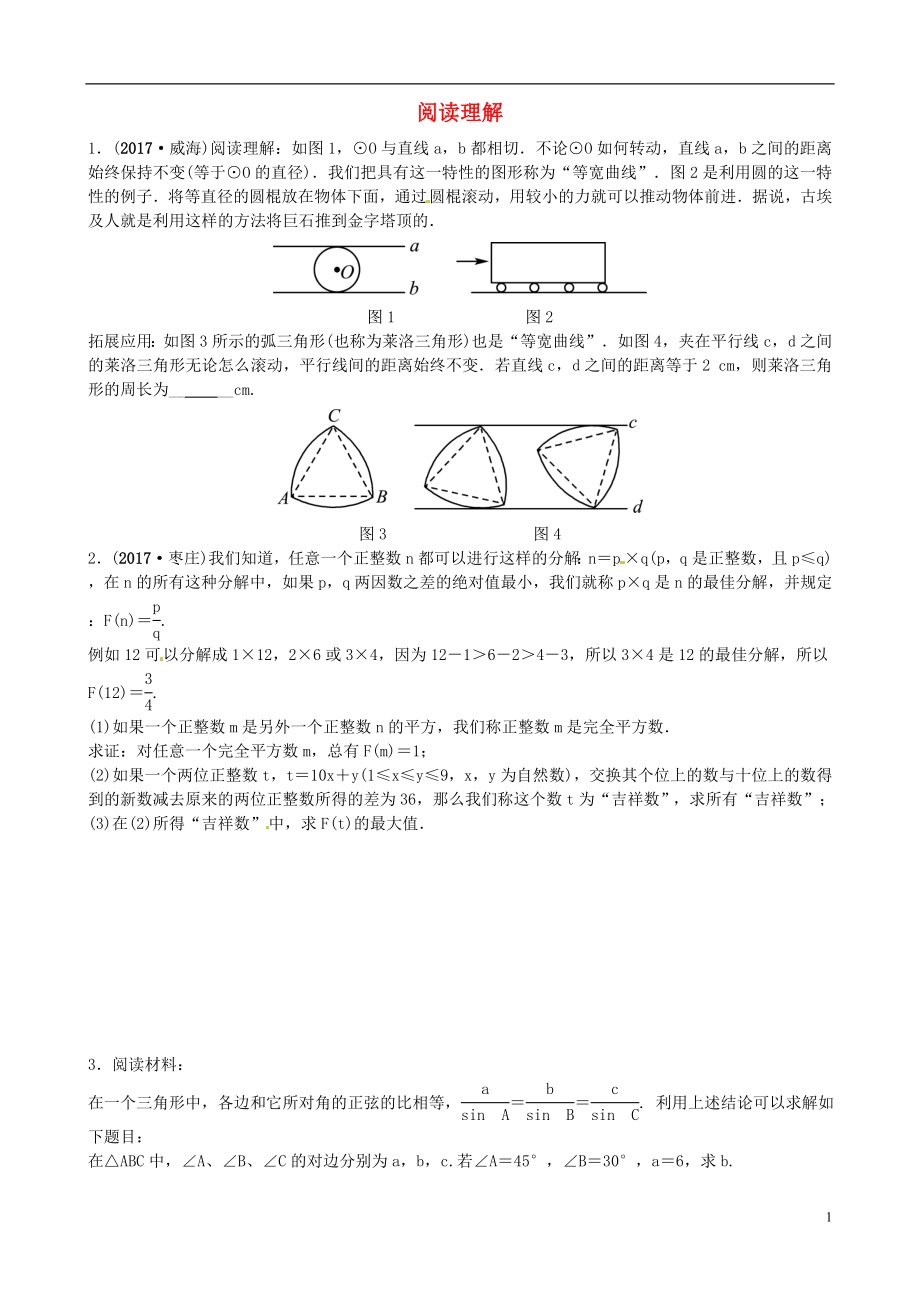
1.(2017·威海)閱讀理解:如圖1�,⊙O與直線a�,b都相切.不論⊙O如何轉(zhuǎn)動,直線a����,b之間的距離始終保持不變(等于⊙O的直徑).我們把具有這一特性的圖形稱為“等寬曲線”.圖2是利用圓的這一特性的例子.將等直徑的圓棍放在物體下面,通過圓棍滾動�,用較小的力就可以推動物體前進(jìn).據(jù)說,古埃及人就是利用這樣的方法將巨石推到金字塔頂?shù)模?
圖1 圖2
拓展應(yīng)用:如圖3所示的弧三角形(也稱為萊洛三角形)也是“等寬曲線”.如圖4��,夾在平行線c��,d之間的萊洛三角形無論怎么滾動,平行線間的距離始終不變.若直線c���,d之間的距離等于2 cm�����,則萊洛三角形的周長為_______
2��、_cm.
圖3 圖4
2.(2017·棗莊)我們知道��,任意一個正整數(shù)n都可以進(jìn)行這樣的分解:n=p×q(p���,q是正整數(shù)��,且p≤q)��,在n的所有這種分解中�����,如果p����,q兩因數(shù)之差的絕對值最小���,我們就稱p×q是n的最佳分解,并規(guī)定:F(n)=.
例如12可以分解成1×12����,2×6或3×4,因?yàn)?2-1>6-2>4-3����,所以3×4是12的最佳分解,所以F(12)=.
(1)如果一個正整數(shù)m是另外一個正整數(shù)n的平方����,我們稱正整數(shù)m是完全平方數(shù).
求證:對任意一個完全平方數(shù)m,總有F(m)=1�����;
(2)如果一個兩位正整數(shù)t��,t=10x+y(1≤x≤y≤9�����,x,y為自然數(shù))���,
3��、交換其個位上的數(shù)與十位上的數(shù)得到的新數(shù)減去原來的兩位正整數(shù)所得的差為36��,那么我們稱這個數(shù)t為“吉祥數(shù)”�����,求所有“吉祥數(shù)”���;
(3)在(2)所得“吉祥數(shù)”中,求F(t)的最大值.
3.閱讀材料:
在一個三角形中��,各邊和它所對角的正弦的比相等�,==. 利用上述結(jié)論可以求解如下題目:
在△ABC中,∠A����、∠B�����、∠C的對邊分別為a,b����,c.若∠A=45°,∠B=30°�����,a=6���,求b.
解:在△ABC中����,∵ =��,
∴b====3.
理解應(yīng)用:
如圖����,甲船以每小時30海里的速度向正北方向航行,當(dāng)甲船位于A1處時��,乙船位于甲船的北偏西105°方向的B1處
4�����、,且乙船從B1處按北偏東15°方向勻速直線航行�,當(dāng)甲船航行20分鐘到達(dá)A2時,乙船航行到甲船的北偏西120°方向的B2處�,此時兩船相距10海里.
(1)判斷△A1A2B2的形狀,并給出證明����;
(2)乙船每小時航行多少海里?
4.(2017·臨沂)數(shù)學(xué)課上��,張老師出示了問題:如圖1�����,AC�,BD是四邊形ABCD的對角線,若∠ACB=∠ACD=∠ABD=∠ADB=60°��,則線段BC�,CD,AC三者之間有何等量關(guān)系���?
經(jīng)過思考���,小明展示了一種正確的思路:如圖2,延長CB到E�����,使BE=CD����,連接AE.證得△ABE≌△ADC,從而容易證明△ACE是等邊三角形.故AC=CE��,所以AC=BC+CD.
5���、
圖1 圖2 圖3
小亮展示了另一種正確的思路:如圖3�,將△ABC繞著點(diǎn)A逆時針旋轉(zhuǎn)60°��,使AB與AD重合����,從而容易證明△ACF是等邊三角形,故AC=CF�����,所以AC=BC+CD.
在此基礎(chǔ)上���,同學(xué)們做了進(jìn)一步的研究:
(1)小穎提出:如圖4���,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改為“∠ACB=∠ACD=∠ABD=∠ADB=45°”���,其他條件不變,那么線段BC���,CD����,AC三者之間有何等量關(guān)系����?針對小穎提出的問題,請你寫出結(jié)論����,并給出證明.
圖4 圖5
(2)小華提出:如圖5,如果把“∠ACB=
6�����、∠ACD=∠ABD=∠ADB=60°”改為“∠ACB=∠ACD=∠ABD=∠ADB=α”�����,其他條件不變�����,那么線段BC�,CD,AC三者之間有何等量關(guān)系���?針對小華提出的問題�����,請你寫出結(jié)論��,不用證明.
5.(2017·濟(jì)寧)定義:點(diǎn)P是△ABC內(nèi)部或邊上的點(diǎn)(頂點(diǎn)除外)�,在△PAB��,△PBC�����,△PCA中��,若至少有一個三角形與△ABC相似,則稱點(diǎn)P是△ABC的自相似點(diǎn).
圖1
例如:如圖1�����,點(diǎn)P在△ABC的內(nèi)部����,∠PBC=∠A,∠BCP=∠ABC��,則△BCP∽△ABC�����,故點(diǎn)P是△ABC的自相似點(diǎn).
請你運(yùn)用所學(xué)知識��,結(jié)合上述材料�����,解決下列問題:
在平面直角坐標(biāo)
7����、系中,點(diǎn)M是曲線y=(x>0)上的任意一點(diǎn),點(diǎn)N是x軸正半軸上的任意一點(diǎn).
(1)如圖2����,點(diǎn)P是OM上一點(diǎn),∠ONP=∠M��,試說明點(diǎn)P是△MON的自相似點(diǎn)��;當(dāng)點(diǎn)M的坐標(biāo)是(�����,3)�,點(diǎn)N的坐標(biāo)是(�����,0)時�����,求點(diǎn)P的坐標(biāo)���;
圖2
圖3
(2)如圖3��,當(dāng)點(diǎn)M的坐標(biāo)是(3��,)��,點(diǎn)N的坐標(biāo)是(2�����,0)時����,求△MON的自相似點(diǎn)的坐標(biāo);
(3)是否存在點(diǎn)M和點(diǎn)N���,使△MON無自相似點(diǎn)���?若存在,請直接寫出這兩點(diǎn)的坐標(biāo)���;若不存在�,請說明理由.
參考答案
1.2π
2.(1)證明:對任意一個完
8��、全平方數(shù)m�����,設(shè)m=n2(n為正整數(shù)).
∵|n-n|=0為最小,∴n×n是m的最佳分解.
∴對任意一個完全平方數(shù)m��,總有F(m)==1.
(2)解:設(shè)交換t的個位上的數(shù)與十位上的數(shù)得到的新數(shù)為t′����,
則t′=10y+x,
∵t為“吉祥數(shù)”�����,
∴t′-t=(10y+x)-(10x+y)=9(y-x)=36�����,
∴y=x+4.
∵1≤x≤y≤9��,x����,y為自然數(shù)��,
∴滿足條件的“吉祥數(shù)”有:15���,26���,37����,48�,59.
(3)解:F(15)=,F(xiàn)(26)=�,F(xiàn)(37)=,
F(48)==����,F(xiàn)(59)=,
∵>>>>�����,
∴所有“吉祥數(shù)”中����,F(xiàn)(t)的最大值是.
3.解:(1
9、)△A1A2B2是等邊三角形.證明如下:
如圖���,連接A1B2.
∵甲船以每小時30海里的速度向正北方向航行����,航行20分鐘到達(dá)A2,
∴A1A2=30×=10.
又∵A2B2=10��,∠A1A2B2=60°���,
∴△A1A2B2是等邊三角形.
(2)如圖�,∵B1N∥A1A2�����,
∴∠A1B1N=180°-∠B1A1A2=180°-105°=75°�,
∴∠A1B1B2=75°-15°=60°.
∵△A1A2B2是等邊三角形,
∴∠A2A1B2=60°���,
A1B2=A1A2=10,
∴∠B1A1B2=105°-60°=45°.
在△B1A1B2中����,
A1B2=10,∠B1A
10���、1B2=45°��,∠A1B1B2=60°�,
由閱讀材料可知,=����,
故B1B2==,
所以乙船每小時航行÷=20(海里).
4.解:(1)BC+CD=AC.
證明:如圖�����,延長CB到E����,使BE=CD,連接AE.
∵∠ACB=∠ACD=∠ABD=∠ADB=45°�,
∴AB=AD,∠BAD+∠BCD=180°�,
∴∠ABC+∠ADC=180°.
又∠ABE+∠ABC=180°.
∴∠ABE=∠ADC,
∴△ABE≌△ADC���,
∴∠AEB=∠ACD=45°���,
∴∠AEB=∠ACB=45°,
∴∠CAE=90°�,
即△ACE是等腰直角三角形��,
∴CE=AC��,∴BC+CD=
11����、AC.
5.解:(1)∵∠ONP=∠M�,∠NOP=∠MON,
∴△ONP∽△OMN�����,
∴點(diǎn)P是△MON的自相似點(diǎn).
如圖1����,過點(diǎn)P作PD⊥x軸于D點(diǎn),
圖1
則tan∠POD==��,
∴∠MON=60°.
∵△ONP∽△OMN����,
∴∠OPN=∠MNO=90°.
在Rt△OPN中����,
OP=ON·cos 60°=�����,
∴OD=OP·cos 60°=×=�����,
PD=OP·sin 60°=×=����,∴P(�����,).
(2)如圖2��,過點(diǎn)M作MH⊥x軸于H點(diǎn)����,
圖2
∵M(jìn)(3,)����,N(2,0)���,
∴OM=2��,直線OM的表達(dá)式為y=x����,ON=MN=2.
∵P1是△MON的自相似點(diǎn),
∴①當(dāng)△P1ON∽△NOM時��,P1O=P1N����,
過點(diǎn)P1作P1Q⊥x軸于Q點(diǎn),
∴OQ=ON=1.
設(shè)P1(1����,y),∵點(diǎn)P1在直線OM上����,
∴y=×1=,∴P1(1�,).
②當(dāng)△P2NM∽△NOM時,=�,
∴P2N= .
易知∠MON=∠OMN=30°,∠ONM=120°,
且P2M=P2N����,
∴P2N⊥x軸����,∴P2的縱坐標(biāo)為.設(shè)P2(x,)��,
∵點(diǎn)P2在直線OM上��,∴=x��,
解得x=2�����,∴P2(2���,).
綜上所述����,△MON的自相似點(diǎn)為(1��,)或(2,).
(3)存在��,M(����,3),N(2�,0).
7
 (淄博地區(qū))2018中考數(shù)學(xué)總復(fù)習(xí) 專題八 閱讀理解試題
(淄博地區(qū))2018中考數(shù)學(xué)總復(fù)習(xí) 專題八 閱讀理解試題