2020年中考數(shù)學(xué)一輪復(fù)習(xí) 基礎(chǔ)考點及題型 專題27 尺規(guī)作圖與命題的證明（含解析）

《2020年中考數(shù)學(xué)一輪復(fù)習(xí) 基礎(chǔ)考點及題型 專題27 尺規(guī)作圖與命題的證明（含解析）》由會員分享，可在線閱讀，更多相關(guān)《2020年中考數(shù)學(xué)一輪復(fù)習(xí) 基礎(chǔ)考點及題型 專題27 尺規(guī)作圖與命題的證明（含解析）（11頁珍藏版）》請在裝配圖網(wǎng)上搜索。

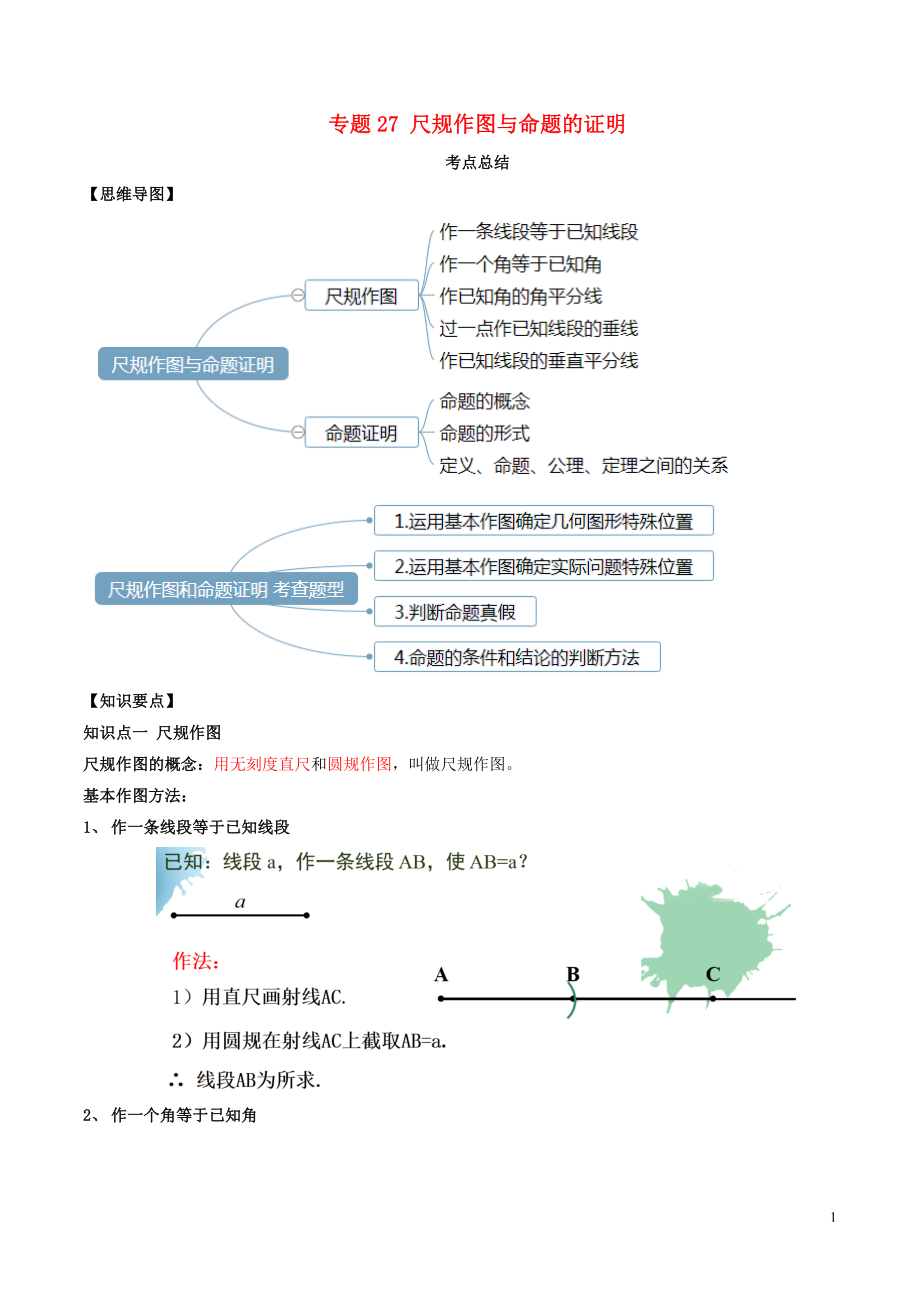
1、專題27 尺規(guī)作圖與命題的證明 考點總結(jié) 【思維導(dǎo)圖】 【知識要點】 知識點一 尺規(guī)作圖 尺規(guī)作圖的概念：用無刻度直尺和圓規(guī)作圖，叫做尺規(guī)作圖。 基本作圖方法： 1、 作一條線段等于已知線段 2、 作一個角等于已知角 3、 作已知角的角平分線 4、 過一點作已知線段的垂線 5、 作已知線段的垂直平分線 【考查題型匯總】 考查題型一 運用基本作圖確定幾何圖形特殊位置 1．（2019·江蘇中考模擬）按要求作圖，并保圖作圖痕跡． 如圖，已知線段a、b、c，用圓規(guī)和直尺作線段AD，使AD=a+2b﹣c． 【答案】見解析. 【詳解】

2、解：如圖所示：AE即為所求． 2．（2019·山東中考模擬）如圖，已知點C是∠AOB的邊OB上的一點，求作⊙P，使它經(jīng)過O、C兩點，且圓心在∠AOB的平分線上． 【答案】見試題解析 【解析】 如圖所示： ． 3．（2019·廣東中考模擬）如圖，在銳角△ABC中，AB＝2cm，AC＝3cm． （1）尺規(guī)作圖：作BC邊的垂直平分線分別交AC，BC于點D、E（保留作圖痕跡，不要求寫作法）； （2）在（1）的條件下，連結(jié)BD，求△ABD的周長． 【答案】（1）作圖見解析；（2）的周長為5cm. 【解析】 （1）如圖，DE為所作； （2）∵DE垂直平分BC，

3、 ∴DB=DC， ∴△ABD的周長=AB+BD+AD=AB+CD+AD=AB+AC=2+3=5（cm）． 4.（2018·山東中考模擬）如圖：求作一點P，使，并且使點P到的兩邊的距離相等． 【答案】見解析 【詳解】 如圖所示：P點即為所求． 5．（2019·江蘇中考模擬）如圖，已知等邊△ABC，請用直尺（不帶刻度）和圓規(guī)，按下列要求作圖（不要求寫作法，但要保留作圖痕跡） （1）作△ABC的外接圓圓心O； （2）設(shè)D是AB邊上一點，在圖中作出一個等邊△DFH，使點F，點H分別在邊BC和AC上； （3）在（2）的基礎(chǔ)上作出一個正六邊形DEFGHI． 【答案】（1）見

4、解析（2）見解析（3）見解析 【詳解】 （1）如圖所示：點O即為所求． （2）如圖所示，等邊△DFH即為所求； （3）如圖所示：六邊形DEFGHI即為所求正六邊形． 6．（2019·吉林東北師大附中中考模擬）圖①、圖②均是8×8的正方形網(wǎng)格，每個小正方形的頂點稱為格點，點A、B、M、N均落在格點上，在圖①、圖②給定的網(wǎng)格中按要求作圖． （1）在圖①中的格線MN上確定一點P，使PA與PB的長度之和最小 （2）在圖②中的格線MN上確定一點Q，使∠AQM＝∠BQM． 要求：只用無刻度的直尺，保留作圖痕跡，不要求寫出作法． 【答案】(1)見解析;(2)見解析. 【詳解】

5、 解：（1）如圖①，作A關(guān)于MN的對稱點A′，連接BA′，交MN于P，此時PA+PB＝PA′+PB＝BA′，根據(jù)兩點之間線段最短，此時PA+PB最??； （2）如圖②，作B關(guān)于MN的對稱點B′，連接AB′并延長交MN于Q，此時∠AQM＝∠BQM． 考查題型二 運用基本作圖確定實際問題特殊位置 1．（2019·甘肅中考模擬）同學(xué)們，數(shù)學(xué)來源于生活又服務(wù)于生活，利用數(shù)學(xué)中的知識可以幫助我們解決許多實際問題.如王明想建一個超市，經(jīng)調(diào)查發(fā)現(xiàn)他家附近有兩個大的居民區(qū)，，同時又有相交的兩條公路，，為方便進(jìn)貨和居民生活，王明想把超市建在到兩居民區(qū)的距離相等，同時到兩公路距離也相等的位置上，繪制了如

6、下的居民區(qū)和公路的位置圖.聰明的你一定能用所學(xué)的數(shù)學(xué)知識幫助王明在圖上確定超市的位置！請用尺規(guī)作圖確定超市點的位置.(作圖不寫作法，但要求保留作圖痕跡) 分析：先將實際問題轉(zhuǎn)化為數(shù)學(xué)問題，把超市看作一個點. 點到，兩點的距離相等，根據(jù)性質(zhì)：__________________， 需用尺規(guī)作出_____________；又點到兩相交直線，的距離相等，根據(jù)性質(zhì)：_________________， 需用尺規(guī)作出_______________；而點同時滿足上述兩個條件，因此應(yīng)該是它們的交點. 請同學(xué)們先完成分析過程(即填空) ，再作圖； 【答案】如圖所示見解析. 線段垂直平分線上的點到線

7、段兩個端點的距離相等，線段的垂直平分線，角平分線上的點到角兩邊的距離相等，的角平分線. 【詳解】 如圖所示， 線段垂直平分線上的點到線段兩個端點的距離相等 線段的垂直平分線 角平分線上的點到角兩邊的距離相等 的角平分線 2．（2019·福建省永春第二中學(xué)初一期末）如圖，在同一平面內(nèi)有四個點A、B、C、D，請按要求完成下列問題．(注：此題作圖不需要寫畫法和結(jié)論) (1)作射線AC； (2)作直線BD與射線AC相交于點O； (3)分別連接AB、AD； (4)我們?nèi)菀着袛喑鼍€段AB、AD、BD的數(shù)量關(guān)系式AB+AD＞BD，理由是______． 【答案】(1)見解析；(

8、2)見解析；(3)見解析；(4)兩點之間，線段最短． 【詳解】 解：(1)(2)(3)如圖所示； (4)AB+AD＞BD理由是：兩點之間，線段最短． 故答案為：兩點之間，線段最短． 知識點二 命題、定理與證明 命題的概念：像這樣判斷一件事情的語句，叫做命題。 命題的形式：“如果…那么…”。（如果+題設(shè)，那么+結(jié)論） 真命題的概念：如果題設(shè)成立，那么結(jié)論一定成立，這樣的命題叫做真命題。 假命題的概念：如果題設(shè)成立，不能保證結(jié)論一定成立，這樣的命題叫做假命題。 如何說明一個命題是假命題：只需要舉出一個反例即可。 定義、命題、公理和定理之間的關(guān)系： 這四者都是句子，都可以

9、判斷真假，即定義、公理和定理也是命題，不同的是定義、公理和定理都是真命題，都可以作為進(jìn)一步判斷其他命題真假的依據(jù)，而命題不一定是真命題，因而它不一定能作為進(jìn)一步判斷其它命題真假的依據(jù)。 一個命題的正確性需經(jīng)過推理，才能作出判斷，這個推理過程叫做證明。 證明的依據(jù)：可以是已知條件，也可以是學(xué)過的定義、基本事實或定理等。 【考查題型匯總】 考查題型三 判斷命題真假 1．（2015·廣東中考真題）下列命題中，真命題的個數(shù)有（ 　） ①對角線互相平分的四邊形是平行四邊形；②兩組對角分別相等的四邊形是平行四邊形； ③一組對邊平行，另一組對邊相等的四邊形是平行四邊形． A．3個 B．2個

10、 C．1個 D．0個 【答案】B 【解析】 試題解析：①對角線互相平分的四邊形是平行四邊形，正確，符合題意； ②兩組對角分別相等的四邊形是平行四邊形，正確，符合題意； ③一組對邊平行，另一組對邊相等的四邊形是平行四邊形，說法錯誤，例如等腰梯形，也符合一組對邊平行，另一組對邊相等． 故選B． 2．（2019·深圳市龍崗區(qū)實驗學(xué)校中考模擬）給出下列5個命題：①兩點之間直線最短；②同位角相等；③等角的補(bǔ)角相等；④不等式組 的解集是﹣2＜x＜2；⑤對于函數(shù)y=﹣0.2x+11，y隨x的增大而增大．其中真命題的個數(shù)是（　　） A．2 B．3 C．4 D．5 【答案】A 【詳解】 ①

11、兩點之間線段最短，故①不正確； ②兩直線平行，同位角相等，故②不正確； ③等角的補(bǔ)角相等，故③正確，是真命題； ④不等式組的解集是﹣2＜x＜2，故④正確，是真命題； ⑤對于函數(shù)y=﹣0.2x+11，y隨x的增大而減小，故⑤不正確． 真命題有③④，共2個． 故選A． 3．（2018·廣東中考模擬）下列命題中： 方程有兩個不相等的實數(shù)根； 不等式的最大整數(shù)解是2； 順次連接對角線相等的四邊形各邊中點得到的四邊形是矩形； 直角三角形的兩條直角邊長分別為6和8，則它的外接圓的半徑為． 其中是真命題的個數(shù)有　　 A．1個 B．2個 C．3個 D．4個 【答案】A 【詳解】

12、 方程，，無實數(shù)根，錯誤； 不等式的解集為，最大整數(shù)解是1，錯誤； 順次連接對角線相等的四邊形各邊中點得到的四邊形是矩形，說法錯誤，應(yīng)為菱形； 直角三角形的兩條直角邊長分別為6和8，則它的外接圓的半徑為，正確； 故選：A． 考查題型四 命題的條件和結(jié)論的判斷方法 1．（2019·互助縣第四中學(xué)初二期末）“兩條直線相交只有一個交點”的題設(shè)是（ ） A．兩條直線 B．相交 C．只有一個交點 D．兩條直線相交 【答案】D 【詳解】 “兩條直線相交只有一個交點”的題設(shè)是兩條直線相交． 故選D． 2．（2018·陜西高新一中初二期中）命題“等角的補(bǔ)角相等”中，

13、“等角的補(bǔ)角”是命題的（ ） A．條件部分 B．是條件，也是結(jié)論 C．結(jié)論部分 D．不是條件，也不是結(jié)論 【答案】A 【詳解】 解：命題“等角的補(bǔ)角相等”: 題設(shè)是兩個角是等角的補(bǔ)角, 結(jié)論是這兩個角相等,故選A. 3.（2018·山東省淄博市臨淄區(qū)金山中學(xué)初一期中）命題“同角的余角相等”改寫成“如果……，那么……”的形式是（ ） A．如果是同角的余角，那么相等 B．如果兩個角是同一個角的余角，那么這兩個角相等 C．如果兩個角是同角，那么這兩個角是余角 D．如果兩個角互余，那么這兩個角相等 【答案】B 【詳解】 命題“同角的余角相等

14、”改寫成“如果…，那么…”的形式是“如果兩個角是同角的余角，那么這兩個角相等”． 故選B． 4．（2017·上海市廊下中學(xué)初二期末）下列定理中，其逆命題是假命題的是( ) A．兩直線平行，內(nèi)錯角相等 B．對頂角相等 C．等腰三角形的兩個底角相等 D．等邊三角形的三個內(nèi)角都是 【答案】B 【解析】 解：A．兩直線平行，內(nèi)錯角相等的逆命題為“內(nèi)錯角相等，兩直線平行”，逆命題為真命題，故此選項錯誤； B．對頂角相等的逆命題為“相等的兩角是對頂角”，逆命題為假命題，符合題意； C．等腰三角形的兩個底角相等的逆命題為“有兩個角相等的三角形是等腰三角形”，逆命題為真命題，故此選項錯誤； D． 等邊三角形的三個內(nèi)角都是60°的逆命題是“三個內(nèi)角都等于60°的三角形是等邊三角形”，逆命題為真命題，故此選項錯誤． 故選B． 11