《2020高中數(shù)學(xué) 第1章1.2.1知能優(yōu)化訓(xùn)練 湘教版必修1》由會(huì)員分享�����,可在線閱讀���,更多相關(guān)《2020高中數(shù)學(xué) 第1章1.2.1知能優(yōu)化訓(xùn)練 湘教版必修1(3頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�。
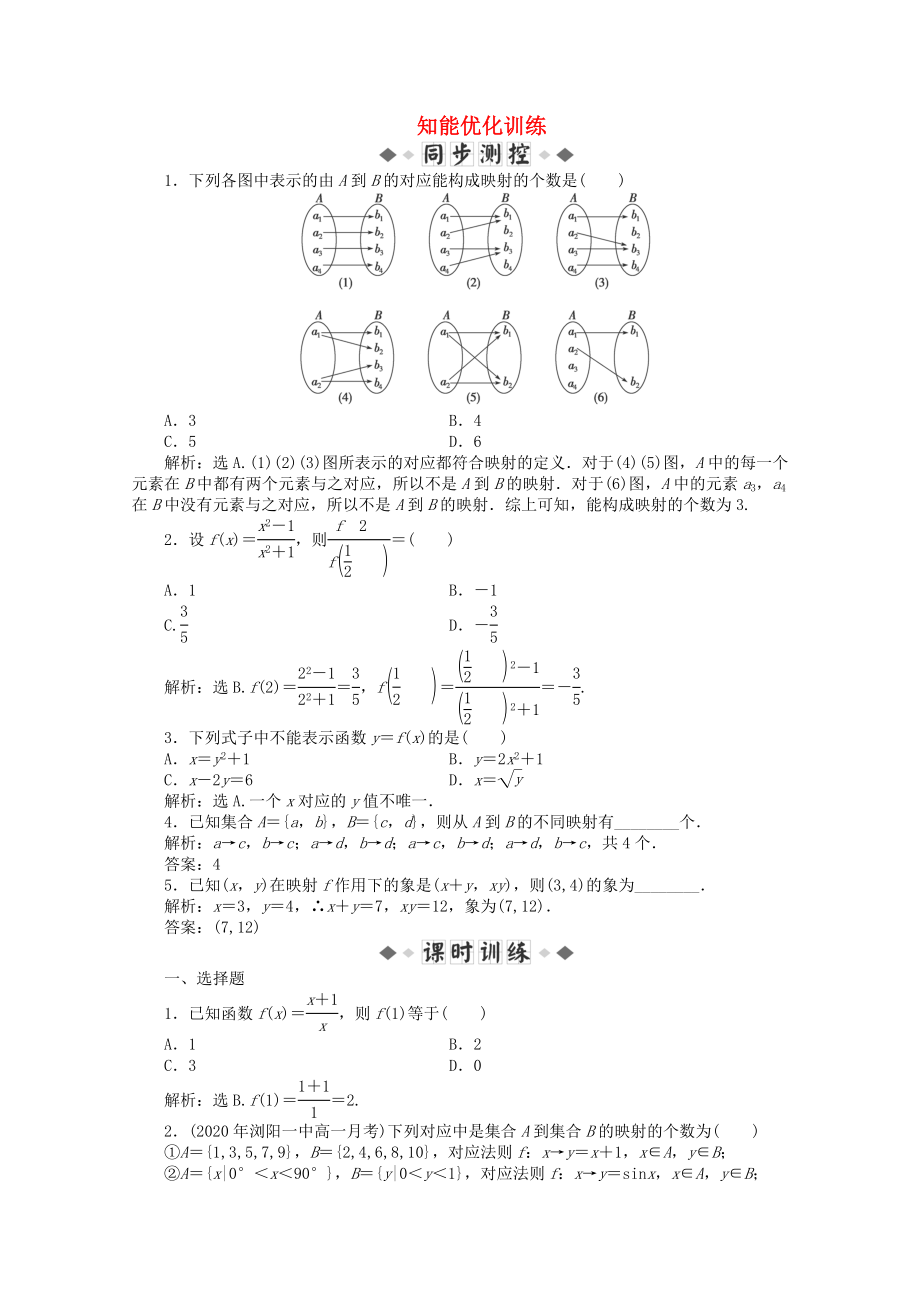
1���、知能優(yōu)化訓(xùn)練1下列各圖中表示的由A到B的對(duì)應(yīng)能構(gòu)成映射的個(gè)數(shù)是()A3B4C5 D6解析:選A.(1)(2)(3)圖所表示的對(duì)應(yīng)都符合映射的定義對(duì)于(4)(5)圖����,A中的每一個(gè)元素在B中都有兩個(gè)元素與之對(duì)應(yīng),所以不是A到B的映射對(duì)于(6)圖��,A中的元素a3��,a4在B中沒有元素與之對(duì)應(yīng)�����,所以不是A到B的映射綜上可知�����,能構(gòu)成映射的個(gè)數(shù)為3.2設(shè)f(x)����,則()A1 B1C. D解析:選B.f(2)�,f.3下列式子中不能表示函數(shù)yf(x)的是()Axy21 By2x21Cx2y6 Dx解析:選A.一個(gè)x對(duì)應(yīng)的y值不唯一4已知集合Aa,b���,Bc���,d�,則從A到B的不同映射有_個(gè)解析:ac����,bc;ad��,b
2���、d����;ac��,bd�����;ad���,bc�����,共4個(gè)答案:45已知(x�����,y)在映射f作用下的象是(xy����,xy),則(3,4)的象為_解析:x3���,y4,xy7�����,xy12�����,象為(7,12)答案:(7,12)一�����、選擇題1已知函數(shù)f(x)����,則f(1)等于()A1 B2C3 D0解析:選B.f(1)2.2(2020年瀏陽(yáng)一中高一月考)下列對(duì)應(yīng)中是集合A到集合B的映射的個(gè)數(shù)為()A1,3,5,7,9���,B2,4,6,8,10,對(duì)應(yīng)法則f:xyx1����,xA,yB�����;Ax|0x90��,By|0y1����,對(duì)應(yīng)法則f:xysinx,xA����,yB;Ax|xR�,By|y0,對(duì)應(yīng)法則f:xyx2���,xA�����,yB.A0 B1C2 D3解析:選D.x1,3,
3���、5,7,9分別對(duì)應(yīng)y2,4,6,8,10���,是映射;xA時(shí)�,yB是映射;對(duì)xA時(shí)��,都有唯一yB�,都是映射3下列哪組中的兩個(gè)函數(shù)是同一函數(shù)()Ay()2與yx By()3與yxCy與y()2 Dy與y解析:選B.A�����、C��、D因定義域不同4設(shè)集合A和集合B都是坐標(biāo)平面上的點(diǎn)集(x����,y)|xR���,yR,映射f:AB把集合A中的元素(x����,y)映射成集合B中的元素(xy,xy)����,則在映射f下,象(2,1)的原象是()A(3,1) B.C. D(1,3)解析:選B.根據(jù)題意有解得所以(2,1)的原象為.5已知f(x)(xR)���,則f(2)等于()A2 BC. D不確定解析:選B.2R�����,f(2).6設(shè)f:xx2是從
4����、集合A到集合B的函數(shù)���,如果B1,2��,則AB()A B或1C1 D或2解析:選B.f:xx2是從集合A到集合B的函數(shù)���,且B1,2�����,集合A為1,1����,或1,1��,或1,1�,或1,或1���,或1��,或1���,或1����,或1,AB,或AB1二�、填空題7點(diǎn)(x,y)在映射f下的象為����,則點(diǎn)(2,0)在f作用下的原象是_解析:由解得答案:(,1)8f(x)����,g(x)x21,則f(2)_��,fg(2)_.解析:f(2)�,g(2)2213,fg(2)f(3).答案:9若f(x)ax2���,a為一個(gè)正的常數(shù)����,且ff()���,則a_.解析:因?yàn)閒()2a.所以ff()f(2a)a(2a)2��,所以a(2a)20(a0)���,故2a0����,所以a.答案:
5��、三�����、解答題10已知集合AR��,B(x�����,y)|x��,yR���,f:AB是從A到B的映射�����,f:x(x1,x21),求A中元素在B中的對(duì)應(yīng)元素和B中元素在A中的對(duì)應(yīng)元素解:將x代入對(duì)應(yīng)法則���,可求出其在B中的對(duì)應(yīng)元素(1,3)由得x.所以在B中的對(duì)應(yīng)元素為(1,3)���,在A中的對(duì)應(yīng)元素為.11下列對(duì)應(yīng)是不是從A到B的映射,為什么��?(1)A(0�����,)��,BR����,對(duì)應(yīng)法則是“求平方根”;(2)Ax|2x2����,By|0y1,對(duì)應(yīng)法則是f:xy(其中xA�,yB);(3)Ax|0x2���,By|0y1���,對(duì)應(yīng)法則是f:xy(x2)2(其中xA��,yB)�����;(4)Ax|xN�,B1,1�����,對(duì)應(yīng)法則是f:xy(1)x(其中xA�����,yB)解:(1)不
6���、是從A到B的映射因?yàn)槿魏握龜?shù)的平方根都有兩個(gè)���,所以對(duì)A中任何一個(gè)元素,在B中都有兩個(gè)元素與之對(duì)應(yīng)(2)是從A到B的映射因?yàn)锳中每個(gè)數(shù)的平方除以4后��,都在B中有唯一的數(shù)與之對(duì)應(yīng)(3)不是從A到B的映射因?yàn)锳中有的元素在B中無(wú)元素與之對(duì)應(yīng)如0A,而(02)24B.(4)是從A到B的映射因?yàn)锳中每一個(gè)元素在B中都有唯一的元素與之對(duì)應(yīng)12下列式子能否確定y是x的函數(shù)���?(1)x2y22;(2)1�;(3)y.解:(1)由x2y22得y,不能確定y是x的函數(shù)���,如當(dāng)x1時(shí)���,由它所確定的y值有兩個(gè)(2)由1,得y(1)21.所以當(dāng)x在x|x1中任取一個(gè)值時(shí)����,由它可以確定唯一的y值與之對(duì)應(yīng),故由它可以確定y是x的函數(shù)(3)由��,得x�����,故由它不能確定y是x的函數(shù)
 2020高中數(shù)學(xué) 第1章1.2.1知能優(yōu)化訓(xùn)練 湘教版必修1
2020高中數(shù)學(xué) 第1章1.2.1知能優(yōu)化訓(xùn)練 湘教版必修1