《江蘇省昆山市兵希中學(xué)中考數(shù)學(xué)一輪總復(fù)習(xí) 第29課時(shí) 梯形(無答案) 蘇科版》由會(huì)員分享�,可在線閱讀,更多相關(guān)《江蘇省昆山市兵希中學(xué)中考數(shù)學(xué)一輪總復(fù)習(xí) 第29課時(shí) 梯形(無答案) 蘇科版(4頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索�。
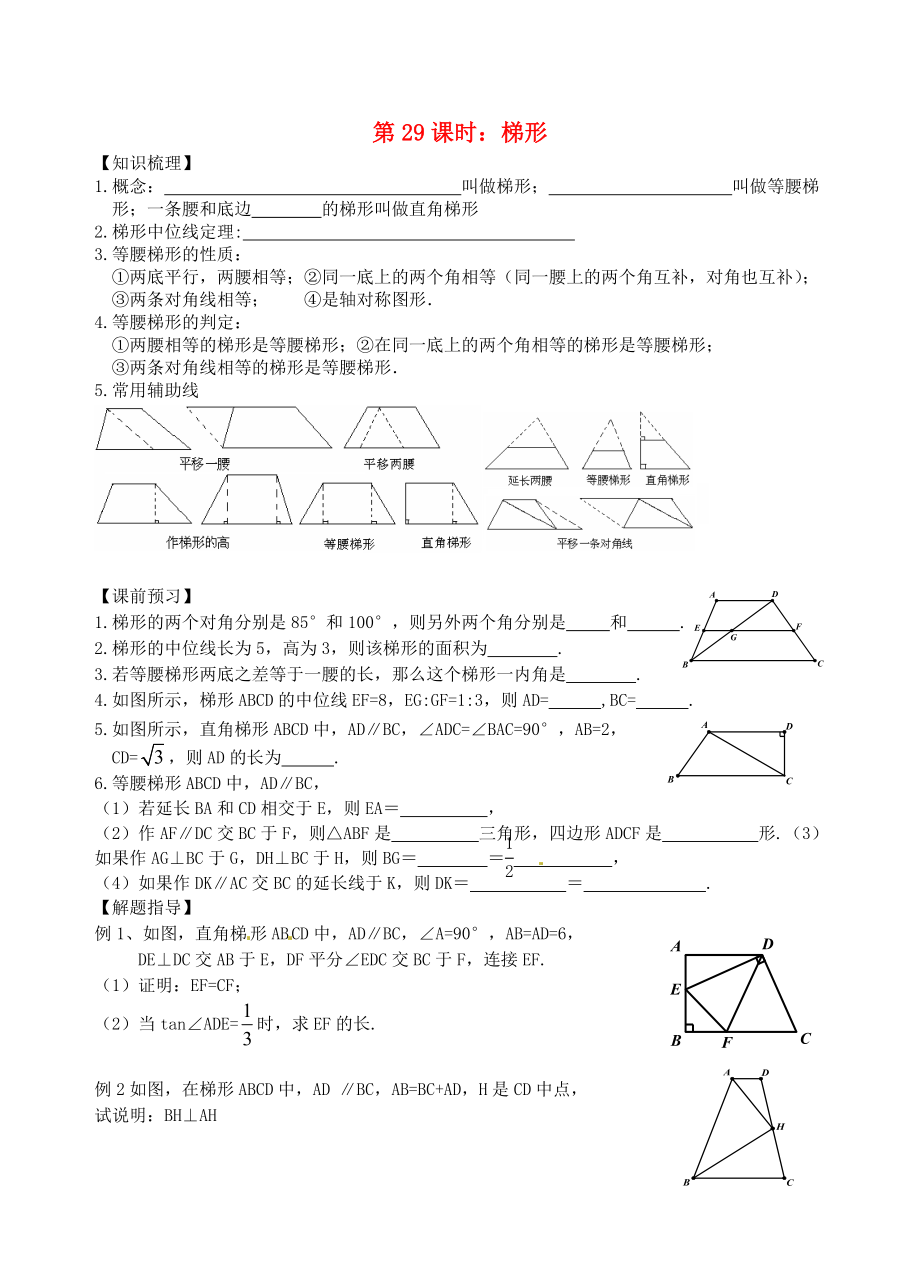
1、第29課時(shí):梯形 【知識(shí)梳理】1.概念: 叫做梯形�����; 叫做等腰梯形���;一條腰和底邊 的梯形叫做直角梯形2.梯形中位線定理: 3.等腰梯形的性質(zhì):兩底平行���,兩腰相等;同一底上的兩個(gè)角相等(同一腰上的兩個(gè)角互補(bǔ)��,對角也互補(bǔ));兩條對角線相等�����; 是軸對稱圖形4.等腰梯形的判定:兩腰相等的梯形是等腰梯形���;在同一底上的兩個(gè)角相等的梯形是等腰梯形����;兩條對角線相等的梯形是等腰梯形5.常用輔助線 【課前預(yù)習(xí)】1.梯形的兩個(gè)對角分別是85和100�����,則另外兩個(gè)角分別是 和 .2.梯形的中位線長為5�,高為3,則該梯形的面積為 .3.若等腰梯形兩底之差等于一腰的長�����,那么這個(gè)梯形一內(nèi)角是 .4.如圖所示��,梯形ABCD的中
2�、位線EF=8,EG:GF=1:3���,則AD= ,BC= .5.如圖所示���,直角梯形ABCD中,ADBC����,ADC=BAC=90,AB=2����, CD=,則AD的長為 .6.等腰梯形ABCD中��,ADBC����,(1)若延長BA和CD相交于E,則EA�����,(2)作AFDC交BC于F���,則ABF是 三角形�,四邊形ADCF是 形.(3)如果作AGBC于G,DHBC于H��,則BG ���,(4)如果作DKAC交BC的延長線于K�,則DK .【解題指導(dǎo)】例1��、如圖��,直角梯形ABCD中�,ADBC,A=90���,AB=AD=6���,DEDC交AB于E,DF平分EDC交BC于F�����,連接EF.(1)證明:EF=CF�;(2)當(dāng)tanADE=時(shí),求EF的長.
3、例2如圖���,在梯形ABCD中�����,AD BC��,AB=BC+AD,H是CD中點(diǎn)���,試說明:BHAH例3如圖����,已知梯形ABCD中����,ADBC,DEBC于點(diǎn)E����,DE=a, DBC=45, ACB=30.求梯形ABCD的面積.例4 如圖,梯形ABCD中����,ADBC�,DCB=45��,CD=2�����,BDCD過點(diǎn)C作CEAB于E���,交對角線BD于F����,點(diǎn)G為BC中點(diǎn)��,連接EG�、AFABEGCDF(1)求EG的長;(2)求證:CF=AB+AF 例5.等腰梯形ABCD中�,ADBC,AB=CD�,AD:BC=5:6,A與D的平分線與BC的交點(diǎn)分BC為三等分��,梯形周長57����,求梯形的上下底的長.【課堂練習(xí)】1.已知四邊形ABCD各個(gè)內(nèi)角度數(shù)
4����、的比為ABCD=2213����,則此四邊形是_.2.梯形兩底的差是4,中位線長是8�����,則上底是����,下底長是����。3.已知梯形的兩底長分別是6,8�,一腰長為7.則另一腰長a的取值范圍是_, 若a為奇數(shù)�����,則此梯形為_ _梯形.4.等腰梯形有一個(gè)角為120,腰長為3cm���,一底邊長為4cm�����,則另一底邊長為_5.梯形ABCD中ADBC,C=70,B=55�,AD=4�,BC=6,則CD的長_ _6.直角梯形一腰長10cm��,則一條腰與底邊所成的角是30����,則另一腰長為 cm.7如圖,在直角梯形ABCD中�,ADBC,ABBC, DCB=75,以CD為一邊的等邊三角形DCE的一頂點(diǎn)E在要AB上.(1)求AED的度數(shù)�;(2)求證:
5、AB=BC.【課后作業(yè)】 班級(jí) 姓名 一����、必做題:1.下面四個(gè)命題中,錯(cuò)誤的命題個(gè)數(shù)是( )(1)有一組對邊平行的四邊形是梯形 (2)有一個(gè)角是直角的梯形是直角梯形(3)有兩個(gè)角相等的梯形是等腰梯形 (4)兩條對角線相等的梯形是等腰梯形(A)1 (B)2 (C)3 (D)02.若梯形的中位線被它的兩條對角線三等分�,則梯形的上底a與下底b(ab)的比是()(A) (B) (C) (D)3.順次連接等腰梯形兩底及兩對角線的中點(diǎn)所得的四邊形是( ) (A)平行四邊形 (B)矩形 (C)菱形 (D)正方形4.直角梯形的一條對角線把梯形分成兩個(gè)三角形�,其中一個(gè)是邊長為30的等邊三角形���,則這個(gè)梯形的中位線
6��、長是( ) (A)15 (B)22.5 (C)45 (D)905.如圖����,梯形ABCD中�����,ADMNGHBC����,AMMGGB,AD12�����,BC28��,則MN十GH( ) (A)30 (B)38 (C)40 (D)466.梯形ABCD中��,ADBC�,AB=CD,BD平分ABC��,BDCD����,延長BA,CD交于E點(diǎn)��,則E的度數(shù)是 7.等腰梯形的腰與中位線的長都是6厘米��,則它的周長是 厘米8.如圖����,把長為10cm的長方形紙片對折,按圖中的虛線剪成梯形并打開����,則打開后,梯形中位線的長 cm9.直角梯形ABCD中����,D90,AD3���,CD4����,且CAAB,則BC ���,梯形面積是 10.如圖�����,ABC中�����,D�����,F(xiàn)��,F(xiàn)分別是各邊中點(diǎn)�����,
7、AGBC于G�����。求證:四邊形DGEF是等腰梯形11.如圖,梯形ABCD中�,AB是下底,以AD�,AC為鄰邊作平行四邊形ADEC,延長DC交BE于F點(diǎn)���。求證:F是BE的中點(diǎn)12.如圖�����,矩形ABCD中�����,AC���,BD交于O點(diǎn),BEAC于E�����,CFBD于F��,且CDF60,CFcm�����。(1)求證:四邊形BCFE是等腰梯形��;(2)求這個(gè)梯形的中位線長�����。二����、選做題:13.等腰梯形的兩條對角線分別垂直于兩腰,一底邊等于腰����,則梯形上底:下底 .14.等腰梯形的腰長是24厘米,一對角線分中位線成8厘米和20厘米���,則此對角線長為 厘米.15.梯形ABCD中�����,ABCD����,AD=BC���,設(shè)ABa�����,DCb�����,BC=c, ACm�����。求證:m2c2ab16.如圖�,梯形ABCD中�,ADBC,BC90���,E���,F(xiàn)分別是AD�,BC的中點(diǎn)�����,求證:EF(BCAD)17.如圖��,在等腰梯形ABCD中�,ABDC,CGAB于G���,對角線ACBC于點(diǎn)O���,EF是中位線,求證CGEF.18.如圖所示����,在直角梯形紙片ABCD中,ABDC����,A=90,CDAD�����,將紙片沿多點(diǎn)D的直線折疊,使點(diǎn)A落在邊CD上的點(diǎn)E處�,折痕為DF,連接EF并展開紙片.(1)求證:四邊形ADEF是正方形����;(2)取線段AF的中點(diǎn)G��,連接EG�,如果BG=CD,試說明四邊形GBCE是等腰梯形.
 江蘇省昆山市兵希中學(xué)中考數(shù)學(xué)一輪總復(fù)習(xí) 第29課時(shí) 梯形(無答案) 蘇科版
江蘇省昆山市兵希中學(xué)中考數(shù)學(xué)一輪總復(fù)習(xí) 第29課時(shí) 梯形(無答案) 蘇科版