《2018高中數(shù)學(xué) 第3章 不等式 第二節(jié) 一元二次不等式學(xué)案 蘇教版必修5》由會員分享,可在線閱讀�,更多相關(guān)《2018高中數(shù)學(xué) 第3章 不等式 第二節(jié) 一元二次不等式學(xué)案 蘇教版必修5(5頁珍藏版)》請在裝配圖網(wǎng)上搜索。
1��、
一元二次不等式
一��、考點突破
知識點
課標(biāo)要求
題型
說明
一元二次不等式
1. 掌握簡單的一元二次不等式的解法��。
2. 掌握一元二次不等式與相應(yīng)的函數(shù)����、方程的關(guān)系。
選擇題
填空題
一元二次不等式是解不等式的基礎(chǔ)����,要認真掌握。并注意體會不等式��、函數(shù)����、方程間的相互轉(zhuǎn)化思想�����。
二、重難點提示
重點:理解一元二次不等式與一元二次方程���、二次函數(shù)的關(guān)系�����;理解一元二次不等式的恒成立問題���;從實際情境中抽象出一元二次不等式模型。
難點:理解二次函數(shù)圖象��、一元二次方程的根與一元二次不等式解集之間的關(guān)系����。
考點一:一元二次不等式及其解集
(1)概念
形如或(
2、其中)的不等式叫做一元二次不等式���。
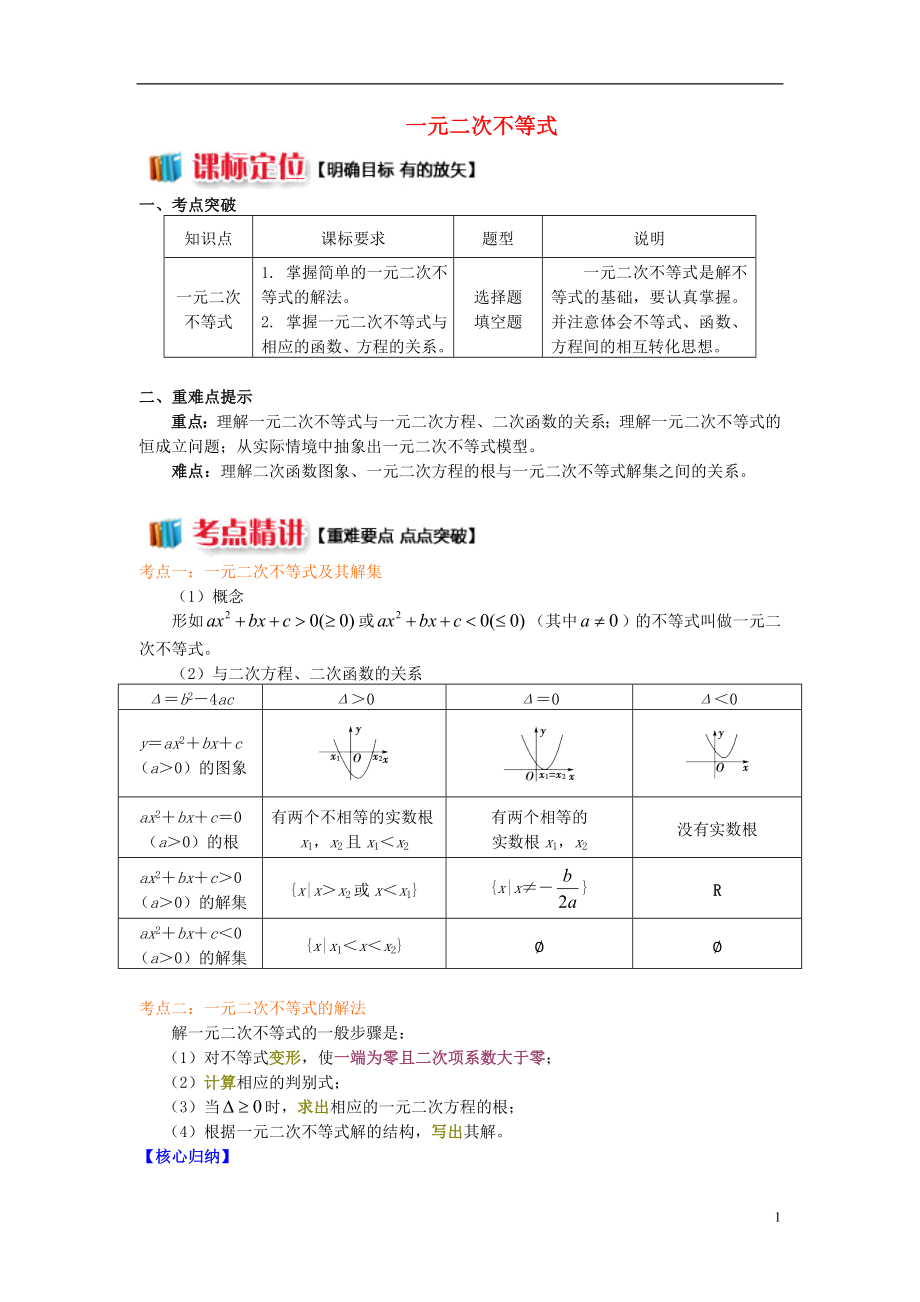
(2)與二次方程��、二次函數(shù)的關(guān)系
Δ=b2-4ac
Δ>0
Δ=0
Δ<0
y=ax2+bx+c
(a>0)的圖象
ax2+bx+c=0
(a>0)的根
有兩個不相等的實數(shù)根x1���,x2且x1<x2
有兩個相等的
實數(shù)根x1,x2
沒有實數(shù)根
ax2+bx+c>0
(a>0)的解集
{x|x>x2或x<x1}
{x|x≠-}
R
ax2+bx+c<0 (a>0)的解集
{x|x1<x<x2}
?
?
考點二:一元二次不等式的解法
解一元二次不等式的一般步驟是:
(1)對不等式變形����,使一端為零且二
3��、次項系數(shù)大于零�����;
(2)計算相應(yīng)的判別式���;
(3)當(dāng)時,求出相應(yīng)的一元二次方程的根���;
(4)根據(jù)一元二次不等式解的結(jié)構(gòu)�����,寫出其解���。
【核心歸納】
其中對的解的結(jié)構(gòu)可記為“”的解為“大于大根或小于小根”,“”的解為“大于小根且小于大根”��,總結(jié)為“大于0取兩邊���,小于0去中間”�����。
【隨堂練習(xí)】若不等式ax2+bx+c>0的解集為{x|-3<x<4}����,求不等式bx2+2ax-c-3b<0的解集�����。
思路分析:由不等式的解集→方程的解→利用韋達定理求a����、b、c關(guān)系→解所求不等式
答案:∵ax2+bx+c>0的解集為{x|-3<x<4}��,
∴a<0且-3和4是方程ax2+bx+c=0的
4��、兩根�。
由韋達定理,得
即
∵不等式bx2+2ax-c-3b<0����,
∴-ax2+2ax+15a<0,即x2-2x -15<0���。
故所求的不等式的解集為{x|-3<x<5}��。
技巧點撥:
1. 一元二次不等式解集的區(qū)間端點值就是相應(yīng)方程的實根��,也是相應(yīng)二次函數(shù)的零點�����,三者之間的相互轉(zhuǎn)化是本題求解的關(guān)鍵�����。
2. 由一元二次不等式解集的情況���,還可判斷出二次項系數(shù)的正負��,解題時也要注意到���。
例題1 (一元二次不等式的基本解法)
解下列不等式:
(1)2x2-3x-2>0;(2) 2x2-4x+7<0��;
(3)-6x2-x+2≥0����;(4)-4x2≥1-4x�����。
思路分析
5、:化一邊為0→二次項系數(shù)化為正→求對應(yīng)方程的根→二次函數(shù)圖象與解集
答案:(1)∵Δ=(-3)2-4×2×(-2)=25>0����,
∴方程2x2-3x-2=0的兩根是-,2��,
∴原不等式的解集為����;
(2)∵Δ=(-4)2-4×2×7<0,
∴不等式2x2-4x+7<0的解集為�;
(3)原不等式可化為6x2+x-2≤0,
∵Δ=12-4×6×(-2)>0�,
∴方程6x2+x-2=0的兩根是-,���,
∴原不等式的解集為�;
(4)原不等式可化為4x2-4x+1≤0����,即(2x-1)2≤0���,
∴原不等式的解集是;
技巧點撥:
1. 本題給出了解一元二次不等式的各種常見類型�,要認真體會
6、�。
2. 一元二次不等式的解集一定要寫成集合或區(qū)間的形式,尤其要注意“>”與“≥”�����,“<”與“≤”符號的區(qū)分��。
例題2 (含參數(shù)的一元二次不等式的解法)
解關(guān)于x的不等式:ax2-(a+1)x+1<0(a∈R)��。
思路分析:當(dāng)a=0時�����,不等式的解集→a<0時�����,不等式的解集→a>0時不等式的解集
答案:若a=0����,原不等式可化為-x+1<0���,
即x>1;
若a<0�,原不等式可化為(x-)(x-1)>0,
即x<或x>1��;
若a>0����,原不等式可化為(x-)(x-1)<0��。(*)
其解的情況應(yīng)由與1的大小關(guān)系決定���,故
(1)當(dāng)a=1時��,由(*)式可得x∈����;
(2)當(dāng)a>1
7���、時��,由(*)式可得<x<1����;
(3)當(dāng)0<a<1時,由(*)式可得1<x<����。
綜上所述:當(dāng)a<0時,解集為{x|x<或x>1}���;
當(dāng)a=0時�����,解集為{x|x>1}����;
當(dāng)0<a<1時�����,解集為{x|1<x<}��;
當(dāng)a=1時�,解集為?;
當(dāng)a>1時,解集為{x|<x<1}���。
技巧點撥:
1. 含參數(shù)的一元二次不等式中��,若二次項系數(shù)為參數(shù)�����,則應(yīng)先考慮二次項系數(shù)是否為零�,然后再討論二次項系數(shù)不為零時的情形�,以便確定解集的形式。
2. 其次對方程的根比較大小����,由根的大小確定參數(shù)的范圍�,然后根據(jù)范圍對參數(shù)分類討論。
例題3 (恒成立問題)
若(m+1)x2-(m-1)x+3(m-
8�、1)<0對任何實數(shù)x恒成立,求實數(shù)m的取值范圍���。
思路分析:對任何實數(shù)x恒成立?不等式解集為實數(shù)集R→討論m+1的取值情況
答案:由題意可知當(dāng)m+1=0�����,即m=-1時�����,
原不等式可化為2x-6<0��,
解得x<3���,不符合題意�,應(yīng)舍去�;
當(dāng)m+1≠0時,由(m+1)x2-(m-1)x+3(m-1)<0對任何實數(shù)x恒成立����,
則有
解得m<-。
綜上所述�����,實數(shù)m的取值范圍是(-∞���,-)��。
技巧點撥:
1. 不等式ax2+bx+c>0的解集是全體實數(shù)(或恒成立)的條件是當(dāng)a=0時�����,b=0�����,c>0����;
當(dāng)a≠0時,
2. 不等式ax2+bx+c<0的解集是全體實數(shù)(或恒成立)的條件是
9�、當(dāng)a=0時,b=0����,c<0;
當(dāng)a≠0時���,
類似地,還有f(x)≤a恒成立?[f(x)]max≤a��;f(x)≥a恒成立?[f(x)]min≥a��。
【綜合拓展】
綜合型不等式的解法
(1)解不等式(x+1)(2-x)(x-3)>0�。
(2)設(shè)a<1,解關(guān)于x的不等式。
思路分析:(1)兩邊都乘以��,再利用根軸法求解�����。
(2)解含參數(shù)的不等式時���,一般要利用轉(zhuǎn)化思想和分類討論思想��,在轉(zhuǎn)化時一定要注意等價性原則���。
答案:(1)原不等式可化為(x+1)(x-2)(x-3)<0,且方程(x+1)(x-2)(x-3)=0的根為x1=-1�����,x2=2����,x3=3,
則由穿針引線法(
10�、如圖)可得原不等式的解集為{x|x<-1或2<x<3}。
(2)原不等式可化為
①當(dāng)a=0時�,化為>0�,
∴-2<x<0���;
②當(dāng)0<a<1時�,化為>0�����,
此時-2<-a<����,∴-2<x<-a或x>。
③當(dāng)a<0時��,化為<0����;
當(dāng)a<-時,有x<-2或<x<-a�;
當(dāng)a=-時,有x<且x≠-2�����;
當(dāng)-<a<0時��,有x<或-2<x<-a���。
綜上所述����,當(dāng)a=0時���,不等式的解集為{x|-2<x<0}��;
當(dāng)0<a<1時�,不等式的解集為{x|-2<x<-a或x>}���;
當(dāng)a<-時���,不等式的解集為{x|x<-2或<x<-a};
當(dāng)a=-時���,不等式的解集為{x|x<且x≠-2}�����;
11����、當(dāng)-<a<0時,不等式的解集為{x|x<或-2<x<-a}�����。
技巧點撥:
解一元高次不等式關(guān)鍵是掌握根軸法的規(guī)則�。
解分式不等式的主要方法是移項、通分���、因式分解���、右邊化為0,利用實數(shù)運算的符號法則等價轉(zhuǎn)化為整式不等式(組)求解�����,本題第二步含有參數(shù)的分式不等式��,解含參數(shù)的不等式要注意以下基本策略:
1. 分清主變量與參變量���,正確實施等價轉(zhuǎn)化��;
2. 在轉(zhuǎn)化過程中���,考慮參數(shù)在取值范圍內(nèi)對運算結(jié)果是否有影響,從哪一步開始對結(jié)果有影響�����,就從哪一步展開對參數(shù)的討論��;
3. 對不同的參數(shù)取值范圍所得的結(jié)果�����,不能取交集�,也不能取并集(因為不是對主變量x的討論),而應(yīng)按參數(shù)分類的方法依次列出�����。
5
 2018高中數(shù)學(xué) 第3章 不等式 第二節(jié) 一元二次不等式學(xué)案 蘇教版必修5
2018高中數(shù)學(xué) 第3章 不等式 第二節(jié) 一元二次不等式學(xué)案 蘇教版必修5