2022年高三數(shù)學(xué)一輪復(fù)習(xí) 《冪函數(shù)》教案 人教大綱版

《2022年高三數(shù)學(xué)一輪復(fù)習(xí) 《冪函數(shù)》教案 人教大綱版》由會員分享，可在線閱讀，更多相關(guān)《2022年高三數(shù)學(xué)一輪復(fù)習(xí) 《冪函數(shù)》教案 人教大綱版（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

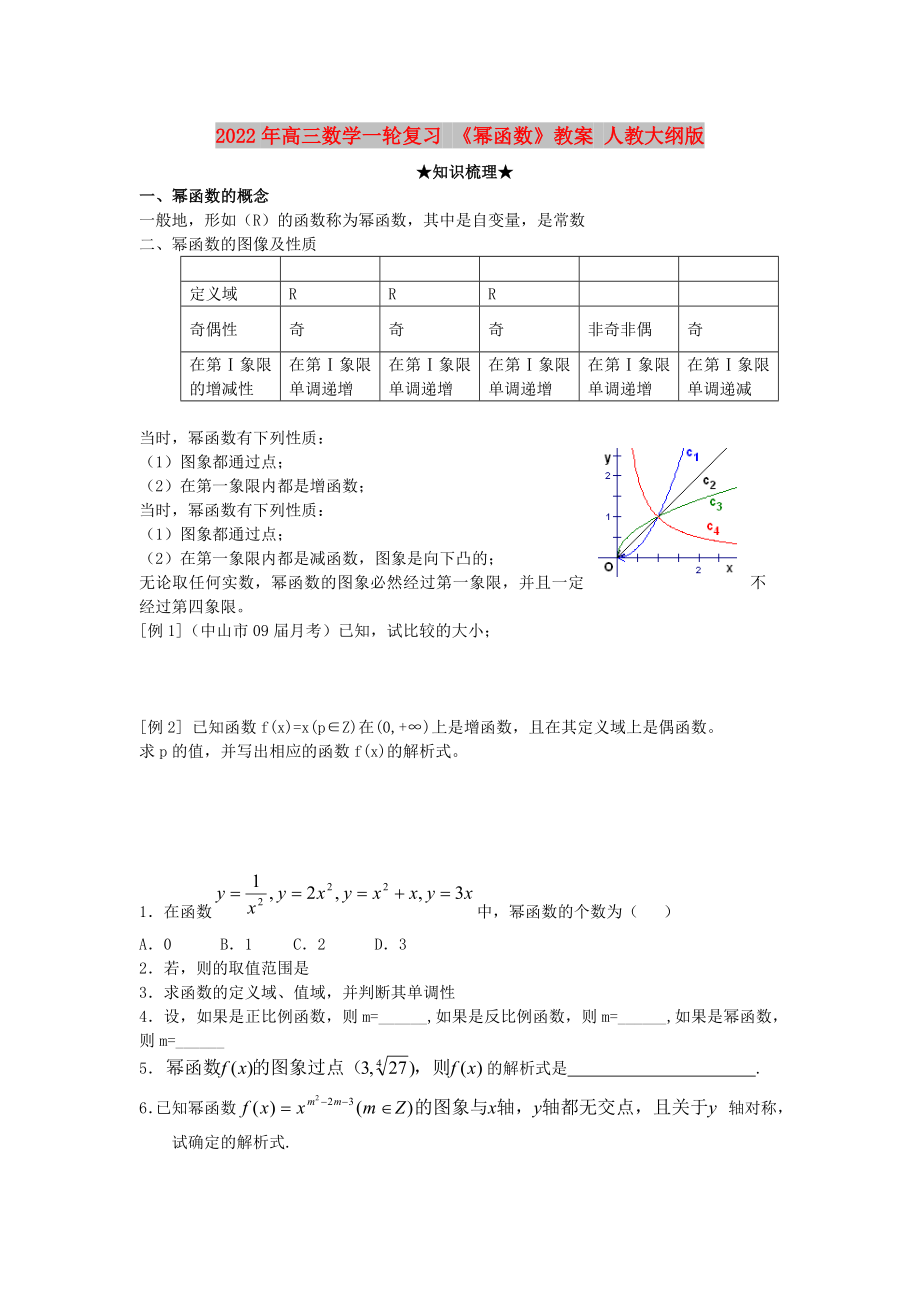
1、2022年高三數(shù)學(xué)一輪復(fù)習(xí) 《冪函數(shù)》教案 人教大綱版 ★知識梳理★ 一、冪函數(shù)的概念 一般地，形如（R）的函數(shù)稱為冪函數(shù)，其中是自變量，是常數(shù) 二、冪函數(shù)的圖像及性質(zhì) 定義域 R R R 奇偶性 奇 奇 奇 非奇非偶 奇 在第Ⅰ象限的增減性 在第Ⅰ象限單調(diào)遞增 在第Ⅰ象限單調(diào)遞增 在第Ⅰ象限單調(diào)遞增 在第Ⅰ象限單調(diào)遞增 在第Ⅰ象限單調(diào)遞減 當(dāng)時，冪函數(shù)有下列性質(zhì)： （1）圖象都通過點； （2）在第一象限內(nèi)都是增函數(shù)； 當(dāng)時，冪函數(shù)有下列性質(zhì)： （1）圖象都通過點； （2）在第一象限內(nèi)都是減函數(shù)，圖象是向

2、下凸的； 無論取任何實數(shù)，冪函數(shù)的圖象必然經(jīng)過第一象限，并且一定不經(jīng)過第四象限。 [例1]（中山市09屆月考）已知，試比較的大小； [例2] 已知函數(shù)f(x)=x(p∈Z)在(0,+∞)上是增函數(shù)，且在其定義域上是偶函數(shù)。 求p的值，并寫出相應(yīng)的函數(shù)f(x)的解析式。 1．在函數(shù)中，冪函數(shù)的個數(shù)為（ ） A．0 B．1 C．2 D．3 2．若，則的取值范圍是 3．求函數(shù)的定義域、值域，并判斷其單調(diào)性 4．設(shè)，如果是正比例函數(shù)，則m=______,如果是反比例函數(shù)，則m=______,如果是冪函數(shù)，則m=______

3、 5．的解析式是 . 6．已知冪函數(shù) 軸對稱，試確定的解析式. 函數(shù)與方程 ★知識梳理★ 一、函數(shù)的零點 方程的實數(shù)根又叫做函數(shù)的零點。 方程有實根函數(shù)的圖像與x軸有交點函數(shù)有零點； ②如果函數(shù)在區(qū)間上的圖像是連續(xù)不斷的，且有，則函數(shù)在區(qū)間上有零點。 二、二分法 1．如果函數(shù)在區(qū)間上的圖像是連續(xù)不斷的一條曲線，且，通過不斷地把函數(shù)的零點所在區(qū)間一分為二，使區(qū)間的兩個端點逐步逼近零點，進而得到零點近似值的方法叫做二分法。 2．給定精度，用二分法求函數(shù)的零點近似值的步驟如下： （1）確定區(qū)間，驗證，給定精度； （2）求區(qū)間的中點； （3）計算：①若，則

4、就是函數(shù)的零點；②若，則令（此時零點）；③若，則令（此時零點 ） （4）判斷是否達(dá)到精度； 即若，則得到零點值（或）；否則重復(fù)步驟（2）-（4） 考點1 零點的求法及零點的個數(shù) [例1] 求函數(shù)的零點. [例2] 求函數(shù)f(x)=lnx＋2x －6的零點個數(shù). 1．（09年浙江五校聯(lián)考）函數(shù)有且僅有一個正實數(shù)的零點，則實數(shù)的取值范圍是（ ） A．；B．；C．；D． 2．（中山市09屆統(tǒng)測）方程的實數(shù)解的個數(shù)為 _______ 3．（湛江市09年高三統(tǒng)考）方程的解所在區(qū)間是（ ） A.（0，1） B.（1

5、，2） C.（2，3） D.（3，4） 4．（金山中學(xué)09屆月考）用二分法求方程在區(qū)間上的近似解，取區(qū)間中點，那么下一個有解區(qū)間為　 5．（xx·惠州調(diào)研）若函數(shù)的一個正數(shù)零點附近的函數(shù)值用二分法計算，其參考數(shù)據(jù)如下： 那么方程的一個近似根（精確到0.1）為（ ）. A．1.2; B．1.3;C．1.4 ; D．1.5 函數(shù)的值域 主要方法： 求函數(shù)的值域的方法常用的有：直接法，配方法，判別式法，基本不等式法，逆求法（反函數(shù)法），換元法，圖像法，利用函數(shù)的單調(diào)性等． （三）例題分析： 例1．求下列函數(shù)的值域： （1）； （2）； （3）； （4）； （5）； （6）；