《內(nèi)蒙古鄂爾多斯市東勝區(qū)培正中學(xué)2013屆中考數(shù)學(xué)專題復(fù)習(xí) 專題十五 勾股定理（無答案） 新人教版》由會(huì)員分享，可在線閱讀，更多相關(guān)《內(nèi)蒙古鄂爾多斯市東勝區(qū)培正中學(xué)2013屆中考數(shù)學(xué)專題復(fù)習(xí) 專題十五 勾股定理（無答案） 新人教版（2頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、
專題十五 勾股定理
【基礎(chǔ)知識(shí)】
1. 勾股定理：如果直角三角形兩直角邊分別為a，b，斜邊為c，那么 .
2. 勾股定理的常見表達(dá)式和變形式：在Rt△ABC中，，、、的對(duì)邊分別是a，b，c，則 ， ， ，進(jìn)而有 ， ， .
3. 勾股定理的逆定理：如果三角形的三邊長(zhǎng)為a、b、c，滿足關(guān)系 ，那么這個(gè)三角形是直角三角形。
【鏈接中考】
例 [人教
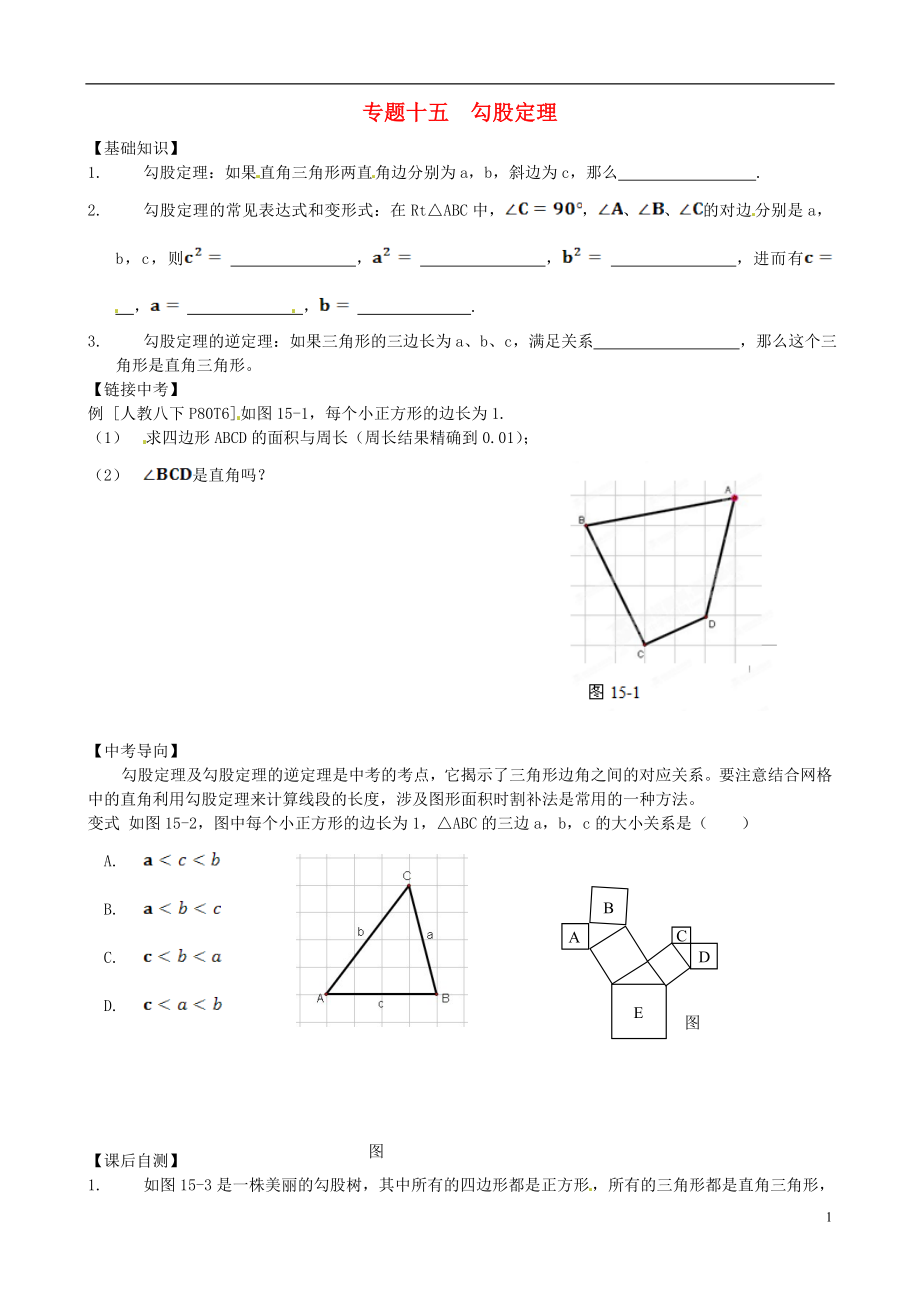
2、八下P80T6]如圖15-1，每個(gè)小正方形的邊長(zhǎng)為1.
（1） 求四邊形ABCD的面積與周長(zhǎng)（周長(zhǎng)結(jié)果精確到0.01）；
（2） 是直角嗎？
【中考導(dǎo)向】
勾股定理及勾股定理的逆定理是中考的考點(diǎn)，它揭示了三角形邊角之間的對(duì)應(yīng)關(guān)系。要注意結(jié)合網(wǎng)格中的直角利用勾股定理來計(jì)算線段的長(zhǎng)度，涉及圖形面積時(shí)割補(bǔ)法是常用的一種方法。
變式 如圖15-2，圖中每個(gè)小正方形的邊長(zhǎng)為1，△ABC的三邊a，b，c的大小關(guān)系是（ ）
A.
A
B
C
D
E
圖15-3
B.
C.
D.
3、
圖15-2
【課后自測(cè)】
1. 如圖15-3是一株美麗的勾股樹，其中所有的四邊形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、D的邊長(zhǎng)分別是3、5、2、3，則最大正方形E的面積是（ ）
A. 13 B. 26 C. 47 D. 94
2. 三角形三邊長(zhǎng)分別為6,8,10，它的最短邊上的高為（ ）
A. 6 B. 4.5 C. 2.4 D. 8
3. 如圖15-4，四邊形ABCD，EFGH，NHMC都是正方形，邊長(zhǎng)分別為a，b，c。A、B、N、E、F五點(diǎn)在同一條直線上，則c= （用含有a，b的代數(shù)式表示）.
M
A
B
N
E
F
H
G
C
D
a
b
c
圖15-4
圖15-5
4. 如圖15-5是由邊長(zhǎng)為1米的正方形地磚鋪設(shè)的地面示意圖，小明沿圖中所示的折線從A到B,到C所走的路程為 .
5. 如圖15-6，一個(gè)牧童在小河的南4米的A處牧馬，而他正位于他的小屋B的西8米北7米處，他想把他的馬牽到小河邊去飲水，然后回家。他要完成這件事所走的最短路程是多少？
2
內(nèi)蒙古鄂爾多斯市東勝區(qū)培正中學(xué)2013屆中考數(shù)學(xué)專題復(fù)習(xí) 專題十五 勾股定理（無答案） 新人教版
