新版高三理科數(shù)學(xué)新課標(biāo)二輪習(xí)題：專題二 函數(shù)與導(dǎo)數(shù) 專題能力訓(xùn)練6 Word版含答案

《新版高三理科數(shù)學(xué)新課標(biāo)二輪習(xí)題：專題二 函數(shù)與導(dǎo)數(shù) 專題能力訓(xùn)練6 Word版含答案》由會員分享，可在線閱讀，更多相關(guān)《新版高三理科數(shù)學(xué)新課標(biāo)二輪習(xí)題：專題二 函數(shù)與導(dǎo)數(shù) 專題能力訓(xùn)練6 Word版含答案（9頁珍藏版）》請在裝配圖網(wǎng)上搜索。

1、 1

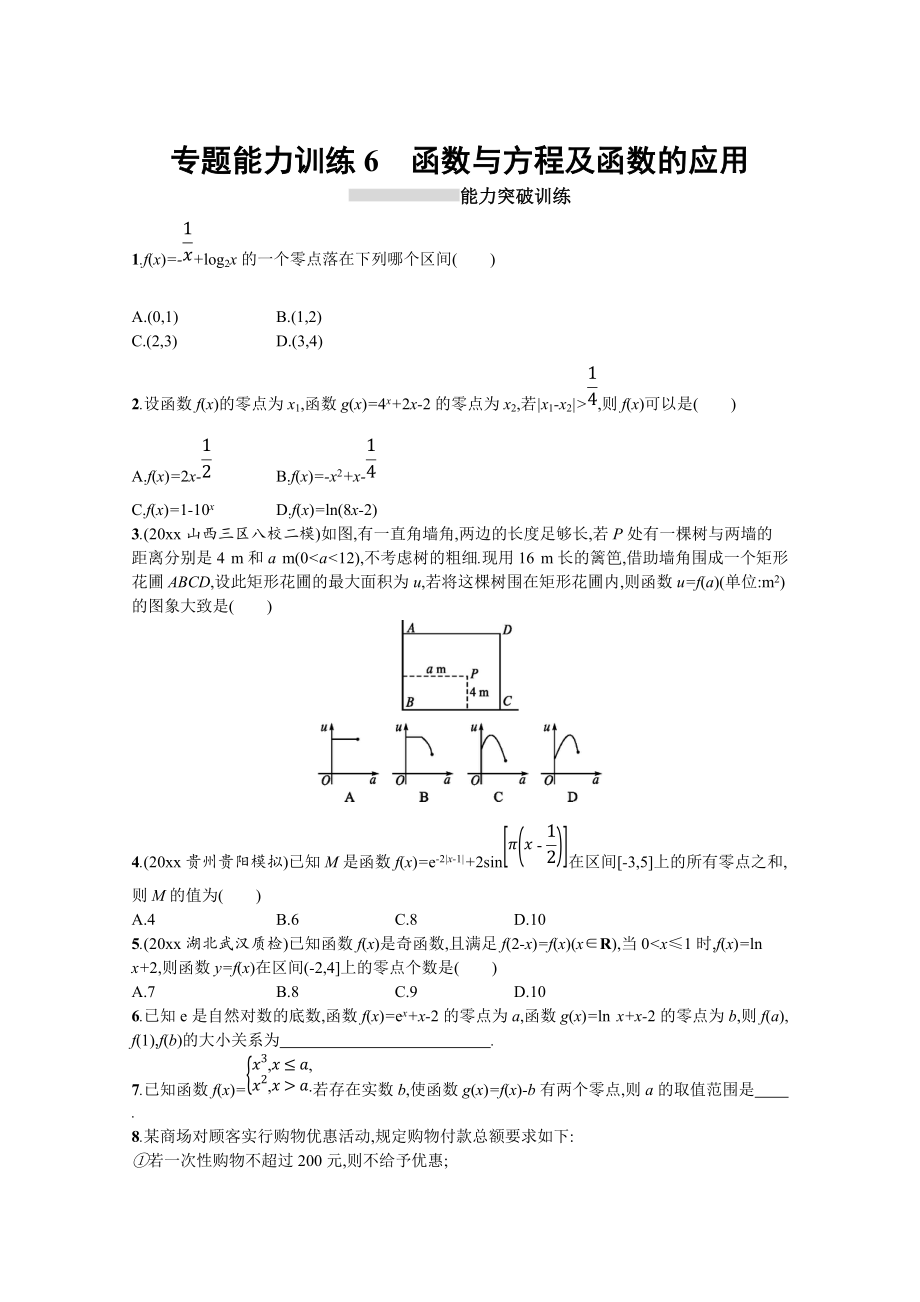
2、 1 專題能力訓(xùn)練6　函數(shù)與方程及函數(shù)的應(yīng)用 能力突破訓(xùn)練 1.f(x)=-1x+log2x的一個零點落在下列哪個區(qū)間(　　) 　　　　　　　　　　　　　　　　　　　 A.(0,1) B.(1,2) C.(2,3) D.(3,4) 2.設(shè)函數(shù)f(x)的零點為x1,函數(shù)g(x)=4x+2x-2的零點為x2,若|x1-x2|>14,則f(x)可以是(　　) A.f(x)=

3、2x-12 B.f(x)=-x2+x-14 C.f(x)=1-10x D.f(x)=ln(8x-2) 3.(20xx山西三區(qū)八校二模)如圖,有一直角墻角,兩邊的長度足夠長,若P處有一棵樹與兩墻的距離分別是4 m和a m(0

4、.10 5.(20xx湖北武漢質(zhì)檢)已知函數(shù)f(x)是奇函數(shù),且滿足f(2-x)=f(x)(x∈R),當(dāng)0a.若存在實數(shù)b,使函數(shù)g(x)=f(x)-b有兩個零點,則a的取值范圍是　　　　　.? 8.某商場對顧客實行購物優(yōu)惠活動,規(guī)

5、定購物付款總額要求如下: ①若一次性購物不超過200元,則不給予優(yōu)惠; ②若一次性購物超過200元但不超過500元,則按標(biāo)價給予9折優(yōu)惠; ③若一次性購物超過500元,則500元按第②條給予優(yōu)惠,剩余部分給予7折優(yōu)惠. 甲單獨購買A商品實際付款100元,乙單獨購買B商品實際付款450元,若丙一次性購買A,B兩件商品,則應(yīng)付款　　　　　元.? 9.已知函數(shù)f(x)=2x,g(x)=12|x|+2. (1)求函數(shù)g(x)的值域; (2)求滿足方程f(x)-g(x)=0的x的值. 10. 如圖,一個長方體形狀的物體E在雨中沿面P(

6、面積為S)的垂直方向做勻速移動,速度為v(v>0),雨速沿E移動方向的分速度為c(c∈R).E移動時單位時間內(nèi)的淋雨量包括兩部分:①P或P的平行面(只有一個面淋雨)的淋雨量,假設(shè)其值與|v-c|×S成正比,比例系數(shù)為110;②其他面的淋雨量之和,其值為12.記y為E移動過程中的總淋雨量.當(dāng)移動距離d=100,面積S=32時, (1)寫出y的表達(dá)式; (2)設(shè)0

7、))=0,g(f(x))=0的實根個數(shù)分別為m,n,則m+n=(　　) A.18 B.16 C.14 D.12 12.已知函數(shù)f(x)=2-|x|,x≤2,(x-2)2,x>2,函數(shù)g(x)=3-f(2-x),則函數(shù)y=f(x)-g(x)的零點個數(shù)為(　　) A.2 B.3 C.4 D.5 13.設(shè)函數(shù)f(x)=2x-a,x<1,4(x-a)(x-2a),x≥1. ①若a=1,則f(x)的最小值為　　　　　;? ②若f(x)恰有2個零點,則實數(shù)a的取值范圍是　　　　　.? 14.已知一家公司生產(chǎn)某種品牌服裝的年固定成本為10萬元,每生產(chǎn)1千件需另投入2.7萬元.設(shè)該公司一年內(nèi)

8、生產(chǎn)該品牌服裝x千件并全部銷售完,每千件的銷售收入為R(x)萬元,且R(x)=10.8-130x2,010. (1)寫出年利潤W(單位:萬元)關(guān)于年產(chǎn)量x(單位:千件)的函數(shù)解析式; (2)當(dāng)年產(chǎn)量為多少千件時,該公司在這一品牌服裝的生產(chǎn)中所獲得的年利潤最大.(注:年利潤=年銷售收入-年總成本) 15.甲方是一農(nóng)場,乙方是一工廠,由于乙方生產(chǎn)須占用甲方的資源,因此甲方有權(quán)向乙方索賠以彌補(bǔ)經(jīng)濟(jì)損失并獲得一定凈收入,在乙方不賠付的情況下,乙方的年利潤x(單位:元)與年產(chǎn)量q(單位:t)滿足函數(shù)關(guān)系:x=2

9、000q.若乙方每生產(chǎn)一噸產(chǎn)品必須賠付甲方s元(以下稱s為賠付價格). (1)將乙方的年利潤w(單位:元)表示為年產(chǎn)量q(單位:t)的函數(shù),并求出乙方獲得最大利潤的年產(chǎn)量; (2)在乙方年產(chǎn)量為q(單位:t)時,甲方每年受乙方生產(chǎn)影響的經(jīng)濟(jì)損失金額y=0.002q2(單位:元),在乙方按照獲得最大利潤的產(chǎn)量進(jìn)行生產(chǎn)的前提下,甲方要在索賠中獲得最大凈收入,應(yīng)向乙方要求的賠付價格s是多少? 參考答案 專題能力訓(xùn)練6　函數(shù)與方程及函數(shù)的應(yīng)用 能力突破訓(xùn)練 1.B　解析由題意得f(x)單調(diào)遞增,f(1)=-1<0,f(2)=12>

10、0,所以f(x)=-1x+log2x的零點落在區(qū)間(1,2)內(nèi). 2.C　解析依題意得g14=2+12-2<0,g12=1>0,則x2∈14,12.若f(x)=1-10x, 則有x1=0,此時|x1-x2|>14,因此選C. 3.B　解析設(shè)AD長為xcm,則CD長為(16-x)cm, 又因為要將點P圍在矩形ABCD內(nèi), 所以a≤x≤12,則矩形ABCD的面積S=x(16-x). 當(dāng)0

11、解析因為f(x)=e-2|x-1|+2sinπx-12=e-2|x-1|-2cosπx,所以f(x)=f(2-x).因為f(1)≠0,所以函數(shù)零點有偶數(shù)個,且兩兩關(guān)于直線x=1對稱.當(dāng)x∈[1,5]時,函數(shù)y=e-2(x-1)∈(0,1],且單調(diào)遞減;函數(shù)y=2cosπx∈[-2,2],且在[1,5]上有兩個周期,因此當(dāng)x∈[1,5]時,函數(shù)y=e-2(x-1)與y=2cosπx有4個不同的交點;從而所有零點之和為4×2=8,故選C. 5.C　解析由函數(shù)f(x)是奇函數(shù)且滿足f(2-x)=f(x)知,f(x)是周期為4的周期函數(shù),且關(guān)于直線x=1+2k(k∈Z)成軸對稱,關(guān)于點(2k,0)(

12、k∈Z)成中心對稱.當(dāng)00恒成立,則函數(shù)f(x)在R上是單調(diào)遞增的, 因為f(0)=e0+0-2=-1<0,f(1)=e1+1-2=e-1>0,所以函數(shù)f(x)的零點a∈(0,1). 由題意,知g'(x)=1x+1>0, 則函數(shù)g(x)在區(qū)間(0,+∞)上是單調(diào)遞增的. 又g(1)=ln1+1-2=-1<0,g

13、(2)=ln2+2-2=ln2>0,則函數(shù)g(x)的零點b∈(1,2). 綜上,可得00,所以,當(dāng)0

14、同的交點. 圖① 圖② 當(dāng)a>1時,由f(x)的圖象(如圖②)知,f(x)在區(qū)間(-∞,a]上遞增,在區(qū)間(a,+∞)上遞增,但a3>a2,所以當(dāng)a21. 8.520　解析設(shè)商品價格為x元,實際付款為y元, 則y=x,0500, 整理,得y=x,0500. ∵0.9×200=180>100, ∴A商品的價格為100元.∵0.9

15、×500=450, ∴B商品的價格為500元.當(dāng)x=100+500=600時,y=100+0.7×600=520,即若丙一次性購買A,B兩件商品,則應(yīng)付款520元. 9.解(1)g(x)=12|x|+2=12|x|+2, 因為|x|≥0,所以0<12|x|≤1, 即20時,由2x-12x-2=0整理,得(2x)2-2·2x-1=0,(2x-1)2=2, 解得2x=1±2.因為2x>0,所以2x=1+2, 即x=log2(1+2).

16、 10.解(1)由題意知,E移動時單位時間內(nèi)的淋雨量為320|v-c|+12,故y=100v320|v-c|+12=5v(3|v-c|+10)(v>0). (2)由(1)知,當(dāng)0

17、故當(dāng)v=c時,ymin=50c. 思維提升訓(xùn)練 11.A　解析由題中圖象知,f(x)=0有3個根0,a,b,且a∈(-2,-1),b∈(1,2);g(x)=0有3個根0,c,d,且c∈(-1,0),d∈(0,1).由f(g(x))=0,得g(x)=0或a,b,由圖象可知g(x)所對每一個值都能有3個根,因而m=9;由g(f(x))=0,知f(x)=0或c,d,由圖象可以看出f(x)=0時對應(yīng)有3個根,f(x)=d時有4個,f(x)=c時只有2個,加在一起也是9個,即n=9,∴m+n=9+9=18,故選A. 12.A　解析因為f(x)=2+x,x<0,2-x,0≤x≤2,(x-2)2,x>

18、2,所以f(2-x)=2+(2-x),2-x<0,2-(2-x),0≤2-x≤2,(2-x-2)2,2-x>2?f(2-x)=x2,x<0,x,0≤x≤2,4-x,x>2, f(x)+f(2-x)=x2+x+2,x<0,2,0≤x≤2,x2-5x+8,x>2, 所以函數(shù)y=f(x)-g(x)=f(x)-3+f(2-x)=x2+x-1,x<0,-1,0≤x≤2,x2-5x+5,x>2. 其圖象如圖所示. 顯然函數(shù)圖象與x軸有2個交點,故函數(shù)有2個零點. 13.①-1　②12,1∪[2,+∞)　解析①當(dāng)a=1時,f(x)=2x-1,x<1,4(x-1)(x-2),x≥1, 當(dāng)x<1

19、時,2x-1∈(-1,1); 當(dāng)x≥1時,4(x-1)(x-2)∈[-1,+∞). 故f(x)的最小值為-1. ②若函數(shù)f(x)=2x-a的圖象在x<1時與x軸有一個交點,則a>0,并且當(dāng)x=1時,f(1)=2-a>0,所以0

20、x≥1上與x軸也無交點,不滿足題意. 當(dāng)21-a≤0,即a≥2時,函數(shù)f(x)=4(x-a)·(x-2a)的圖象與x軸的兩個交點x1=a,x2=2a都滿足題意. 綜上,a的取值范圍為12,1∪[2,+∞). 14.解(1)當(dāng)010時,W=xR(x)-(10+2.7x)=98-10003x-2.7x. 故W=8.1x-x330-10,010. (2)①當(dāng)00;當(dāng)x∈(9,10]

21、時,W'<0. 所以當(dāng)x=9時,W取得最大值, 即Wmax=8.1×9-130×93-10=38.6. ②當(dāng)x>10時,W=98-10003x+2.7x≤98-210003x×2.7x=38, 當(dāng)且僅當(dāng)10003x=2.7x,即x=1009時,W取得最大值38. 綜合①②知:當(dāng)x=9時,W取得最大值38.6, 故當(dāng)年產(chǎn)量為9千件時,該公司在這一品牌服裝的生產(chǎn)中所獲的年利潤最大. 15.解(1)因為賠付價格為s元/噸,所以乙方的實際年利潤為w=2000q-sq(q≥0). 因為w=2000q-sq=-sq-1000s2+10002s, 所以當(dāng)q=1000s2時,w取得最大值.所以乙方取得最大利潤的年產(chǎn)量q=1000s2t. (2)設(shè)甲方凈收入為v元,則v=sq-0.002q2, 將q=1000s2代入上式,得到甲方凈收入v與賠付價格s之間的函數(shù)關(guān)系式: v=10002s-2×10003s4. 又v'=-10002s2+8×10003s5=10002(8000-s3)s5, 令v'=0得s=20.當(dāng)s<20時,v'>0;當(dāng)s>20時,v'<0.所以當(dāng)s=20時,v取得最大值. 因此甲方向乙方要求賠付價格s為20元/噸時,獲最大凈收入.